题目内容
抛物线y=3x2-4x+1与坐标轴的交点个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：抛物线与x轴的交点
专题：
分析：先令3x2-4x+1=0，再求出△的值，进而可得出结论．
解答：解：令3x2-4x+1=0，
∵△=（-4）2-12=16-12=4＞0，
∴抛物线y=3x2-4x+1与x轴有两个交点，与y轴有一个交点．
故选D．
∵△=（-4）2-12=16-12=4＞0，
∴抛物线y=3x2-4x+1与x轴有两个交点，与y轴有一个交点．
故选D．
点评：本题考查的是抛物线与x轴的交点问题，熟知二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系是解答此题的关键．
练习册系列答案
相关题目
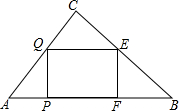如图，在Rt△ABC中，∠C=90°，AC=30cm，BC=40m，矩形EFPQ的四个定点分别在三边上．设EF=xm，矩形EFPQD的面积为ym2，当x为何值时，y的值最大？最大值是多少？
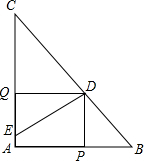在Rt△ABC中，∠A=90°，AB=6，AC=8，点D为BC的中点，DE⊥BC交边AC与点E，点P为射线AB上一动点，点Q为AC上一动点，且∠PDQ=90°．若BP=2，求CQ的长．
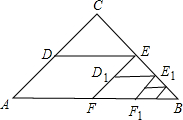如图，△ABC中，∠C=90°，AC=BC=2，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的面积记作S2．照此规律作下去，则S2012=