题目内容
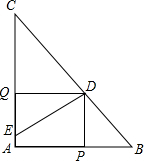 在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为BC的中点,DE⊥BC交边AC与点E,点P为射线AB上一动点,点Q为AC上一动点,且∠PDQ=90°.若BP=2,求CQ的长.
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为BC的中点,DE⊥BC交边AC与点E,点P为射线AB上一动点,点Q为AC上一动点,且∠PDQ=90°.若BP=2,求CQ的长.考点:相似三角形的判定与性质
专题:分类讨论
分析:首先证明△CDE∽△CAB,利用相似三角形的性质求得DE和CE的长,然后分P在线段AB上和AB的延长线上两种情况进行讨论,根据△DBP和△DEQ相似的性质求解.
解答:解:∵DE⊥BC,∠A=90°,
∴∠CDE=∠A=90°,
又∵∠C=∠C,
∴△CDE∽△CAB,
∴
=
=
,
∴DE=
,CE=
;
当点P在线段AB上时,可证△DBP∽△DEQ,
∴
=
,
∴EQ=
,
∴CQ=CE-EQ=
;
当点P在线段AB的延长线上时,△DBP∽△DEQ,
∴
=
,
∴EQ=
,
∴CQ=CE+EQ=
.
∴∠CDE=∠A=90°,
又∵∠C=∠C,
∴△CDE∽△CAB,
∴
| CD |
| AC |
| DE |
| AB |
| CE |
| CB |
∴DE=
| 15 |
| 4 |
| 25 |
| 4 |
当点P在线段AB上时,可证△DBP∽△DEQ,
∴
| BP |
| EQ |
| DB |
| DE |
∴EQ=
| 3 |
| 2 |
∴CQ=CE-EQ=
| 19 |
| 4 |
当点P在线段AB的延长线上时,△DBP∽△DEQ,
∴
| BP |
| EQ |
| DB |
| DE |
∴EQ=
| 3 |
| 2 |
∴CQ=CE+EQ=
| 31 |
| 4 |
点评:本题考查了相似三角形的判定和性质,利用相似三角形的对应边的比相等是常用的求线段的长度的方法,正确进行分类讨论是关键.

练习册系列答案
相关题目
抛物线y=3x2-4x+1与坐标轴的交点个数为( )
| A、0 | B、1 | C、2 | D、3 |
如图1是玩具拼图模板的一部分,已知△ABC的六个元素,则图2中甲、乙、丙三个三角形中能和△ABC完全重合的是( )
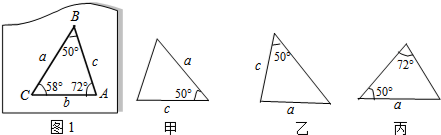
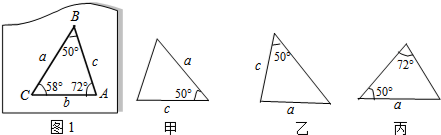
| A、甲和丙 | B、丙和乙 |
| C、只有甲 | D、只有丙 |
 如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为
如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为 已知如图:D、E分别为AB、AC的中点,则S△ADE:S梯形DBCE=
已知如图:D、E分别为AB、AC的中点,则S△ADE:S梯形DBCE= (1)解方程:2x2-3x=0;
(1)解方程:2x2-3x=0; 一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是1米,测得OC⊥AB,垂足为C,且OC=0.3米,则水平面宽AB=
一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是1米,测得OC⊥AB,垂足为C,且OC=0.3米,则水平面宽AB=