题目内容
△ABC和△A′B′C′中,
=
=
=
,且△ABC的周长与△A′B′C′的周长相差8,这两个三角形的周长各为多少?
| AB |
| A′B′ |
| BC |
| B′C′ |
| AC |
| A′C′ |
| 1 |
| 2 |
考点:相似三角形的判定与性质
专题:
分析:由三边对应成比例可判定两三角形相似,且相似比为
,利用相似三角形的周长比等于相似比可得出两三角形的周长比,再结合条件相差8可求得周长.
| 1 |
| 2 |
解答:解:∵
=
=
=
,
∴△ABC∽△A′B′C′,
∴
=
,
∵△ABC的周长与△A′B′C′的周长相差8,
∴△ABC的周长为8,△A′B′C′的周长为16.
| AB |
| A′B′ |
| BC |
| B′C′ |
| AC |
| A′C′ |
| 1 |
| 2 |
∴△ABC∽△A′B′C′,
∴
| l△ABC |
| l△A′B′C′ |
| 1 |
| 2 |
∵△ABC的周长与△A′B′C′的周长相差8,
∴△ABC的周长为8,△A′B′C′的周长为16.
点评:本题主要考查相似三角形的判定和性质,由条件得出两三角形相似是解题的关键.

练习册系列答案
相关题目
抛物线y=3x2-4x+1与坐标轴的交点个数为( )
| A、0 | B、1 | C、2 | D、3 |
3点半钟时,钟表的时针与分针的夹角是( )
| A、30° | B、45° |
| C、60° | D、75° |
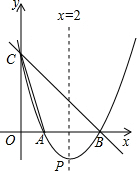 如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2. 如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为
如图,直线AB与坐标轴交于A(1,0)、B(0,2)两点,过A,B两点的抛物线与x轴的另一交点为(3,0),P为抛物线上的一动点,当∠PBA=45°时,P点的坐标为 (1)解方程:2x2-3x=0;
(1)解方程:2x2-3x=0;