题目内容
温州某家电商场计划用5.88万元购进某品牌MP5、手机、游戏机共50件,三种产品的进价和售价如下表所示:
(1)在不超出现有资金前提下,若购进MP5的数量和手机的数量相同,且MP5的数量不超过游戏机的2倍,请问商场有哪几种进货方案?
(2)准备在“五一黄金周”促销活动,商家针对这三种产品推出“现金每购满1000元送50元家电消费券一张,多买多送”的活动,在(1)的条件下,若三种产品在活动期间全部售出,商家预估最多送出消费券多少张?
| 价格 种类 | 进价(元/件) | 售价(元/件) |
| MP5 | 300 | 350 |
| 手机 | 1800 | 2000 |
| 游戏机 | 1500 | 1600 |
(2)准备在“五一黄金周”促销活动,商家针对这三种产品推出“现金每购满1000元送50元家电消费券一张,多买多送”的活动,在(1)的条件下,若三种产品在活动期间全部售出,商家预估最多送出消费券多少张?
考点:二次函数的应用,一元一次不等式组的应用
专题:
分析:(1)设购进PM5x件,购手机x件,则购进游戏机(50-2x)件,根据MP5的数量不超过游戏机的2倍,购买的总费用不超过5.88万元建立不等式组,求出其解即可;
(2)设全部售出的总费用为W元,根据总价=MP5的售价+手机的售价+游戏机售价就可以得出W与x的关系式,由一次函数的性质就可以求出结论.
(2)设全部售出的总费用为W元,根据总价=MP5的售价+手机的售价+游戏机售价就可以得出W与x的关系式,由一次函数的性质就可以求出结论.
解答:解:(1)设购进PM5x件,购手机x件,则购进游戏机(50-2x)件,
由题意可得:
,
解得:18≤x≤20,
∵x为整数,
∴x=18,19,20,
∴共有3种进货方案.
方案1,购进PM5有18件,购手机18件,购游戏机14件,
方案2,购进PM5有19件,购手机19件,购游戏机12件,
方案3,购进PM5有20件,购手机20件,购游戏机10件,
(2)设售出的总额为W元,
W=350x+2000x+1600(50-2x),
W=-850x+80000.
∵k=-850<0,18≤x≤20,
∴当x=18的时候,W取得最大值为64700元,
∵购满1000元才赠券,
∴共送出64张券.
由题意可得:
|
解得:18≤x≤20,
∵x为整数,
∴x=18,19,20,
∴共有3种进货方案.
方案1,购进PM5有18件,购手机18件,购游戏机14件,
方案2,购进PM5有19件,购手机19件,购游戏机12件,
方案3,购进PM5有20件,购手机20件,购游戏机10件,
(2)设售出的总额为W元,
W=350x+2000x+1600(50-2x),
W=-850x+80000.
∵k=-850<0,18≤x≤20,
∴当x=18的时候,W取得最大值为64700元,
∵购满1000元才赠券,
∴共送出64张券.
点评:本题考查了列一元一次不等式组解实际问题的运用一元一次不等式组的解法的运用,一次函数的性质的运用,解答时建立一次函数的解析式是关键.

练习册系列答案
相关题目
抛物线y=3x2-4x+1与坐标轴的交点个数为( )
| A、0 | B、1 | C、2 | D、3 |
3点半钟时,钟表的时针与分针的夹角是( )
| A、30° | B、45° |
| C、60° | D、75° |
如图1是玩具拼图模板的一部分,已知△ABC的六个元素,则图2中甲、乙、丙三个三角形中能和△ABC完全重合的是( )
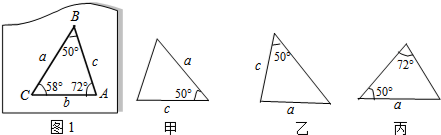
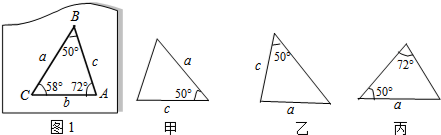
| A、甲和丙 | B、丙和乙 |
| C、只有甲 | D、只有丙 |
函数y=-x2-4x+3图象顶点坐标是( )
| A、(2,-7) |
| B、(2,7) |
| C、(-2,-7) |
| D、(-2,7) |
 如图,以O为圆心的同心圆中,大圆的弦AB交小圆于C、D两点,求证:
如图,以O为圆心的同心圆中,大圆的弦AB交小圆于C、D两点,求证: