题目内容
10.在△ABC中,∠B=∠C,(1)如图1,点D、E分别在BC与AC上,∠ADE=∠AED,求证:∠BAD=2∠CDE;
(2)如图2,将∠CAH沿AH翻折到∠QAH,AH⊥QF于H,QH交BC于F,BP平分∠ABC,QP平分∠AQF,BP与QP交于P,试探究∠P与∠BFQ的关系.
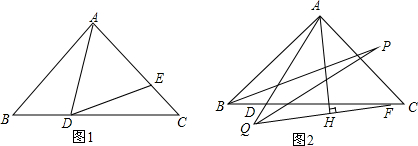
分析 (1)根据三角形的内角和定理得出∠BAD=180°-2∠C-∠DAC,∠DAC=180°-∠ADE-∠AED,由三角形的外角等于和它不相邻的两个内角的和可得∠AED=∠C+∠CDE,从而可以得到结论成立.
(2)根据△BOC和△QOF中,∠BOP=∠QOF,可知∠1+∠P=∠2+∠BFQ,又因为BP平分∠ABC,QP平分∠AQF,进行变化,便可得到∠P与∠BFQ的关系.
解答 (1)证明:∵∠ABC=∠ACB,
∴在△ABC中,∠BAD=180°-2∠C-∠DAC,
∵∠ADE=∠AED,
∴∠BAD=180°-2∠C-∠DAC=180°-2∠C-(180°-2∠AED)=180°-2∠C-180°+2∠AED=-2∠C+2(∠CDE+∠C)=2∠CDE.
(2)解:如图所示:
由题意可得,∠ABC=∠ACB,∠ABC=2∠1,∠AQC=∠ACQ,∠AQC=2∠2,∠ACQ=∠ACB+∠BFQ,
又∵∠BOP=∠QOC,
∴∠1+∠P=∠2+∠BFQ.
即$\frac{1}{2}∠ACB+∠P=\frac{1}{2}∠ACQ+∠BFQ$.
∵∠ACQ=∠ACB+∠BFQ,
∴∠P=$\frac{3}{2}$∠BFQ.
点评 此题考查三角形的外角性质及三角形的内角和定理,角平分线的性质.解题的关键是熟练掌握三角形的外角性质定理,即三角形的一个外角等于与它不相邻的两个内角之和.

练习册系列答案
相关题目
18.关于二次函数y=-2x2+4x+1,下列说法正确的是( )
| A. | 图象是开口向上的抛物线 | |
| B. | 图象对称轴是直线:x=-1 | |
| C. | 点A(x1,y1)和点B(x2,y2)是图象上的两个点,若x1<x2<-1,则y1<y2 | |
| D. | 图象可由y=-2x2的图象向左平移1个单位,再向下平移3个单位得到 |
 已知,圆的半径为4cm,求圆内等边三角形的边长.
已知,圆的半径为4cm,求圆内等边三角形的边长.
 现有可建造50m围墙的材料.准备依靠原有的旧墙(墙体最大长a=23m)围成如图所示仓库试问:
现有可建造50m围墙的材料.准备依靠原有的旧墙(墙体最大长a=23m)围成如图所示仓库试问: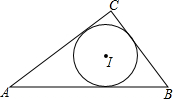 如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.
如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.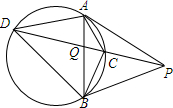 已知P为⊙O外-点,过P作⊙O的切线PA、PB.A、B为切点,直线PCD为⊙O的-条割线,PD交AB于点Q
已知P为⊙O外-点,过P作⊙O的切线PA、PB.A、B为切点,直线PCD为⊙O的-条割线,PD交AB于点Q