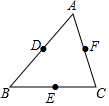如图.在△ABC中.D.E.F分别是AB.BC.CA的中点.以这些点为顶点.在图中能画平行四边形的个数是( )A．2B．3C．4D．5 题目和参考答案——青夏教育精英家教网—

题目内容

5．

如图，在△ABC中，D，E，F分别是AB，BC，CA的中点，以这些点为顶点，在图中能画平行四边形的个数是（　　）

A．

B．

C．

D．

分析由于D、E、F分别是边AB，BC，CA的中点，易知DE、DF、EF都是△ABC的中位线，那么DE∥AC，DF∥BC，EF∥AB，根据平行四边形的定义，两两结合易证四边形EDFC是平行四边形；四边形EBDF是平行四边形；四边形ADEF是平行四边形．

解答解：∵D、E、F分别是边AB，BC，CA的中点，
∴DE、DF、EF都是△ABC的中位线，
∴DE∥AC，DF∥BC，EF∥AB，
∴四边形EDFC是平行四边形，四边形EBDF是平行四边形，四边形ADEF是平行四边形．
故选B．

点评本题考查了平行四边形的判定、三角形中位线定理，解题的关键是熟练掌握三角形中位线定理的内容．

练习册系列答案

中考达标学案系列答案

黑皮系列分层强化训练系列答案

全品新阅读系列答案

150加50篇英语完形填空与阅读理解系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

13．

如果一条抛物线y=ax²+bx+c（a≠0）与x轴的两个交点为A，B（点A在点B的左侧），顶点为P，连接PA，PB，那么称△PAB为这条抛物线的“抛物线三角形”．
（1）请写出“抛物线三角形”是等腰直角三角形时，抛物线的表达式（写出一个即可）；
（2）若抛物线y=-x²+bx（b＞0）的“抛物线三角形”是等边三角形，求b的值；
（3）若抛物线y=ax²+bx+c（a≠0）不存在“抛物线三角形”，则a、b、c之间应满足怎样的关系式？请直接写出．

20．我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．

（1）写出你所学过的特殊四边形中是勾股四边形的两种图形的名称矩形，正方形；
（2）如图1，已知格点（小正方形的顶点）O（0，0），A（3，0），B（0，4），请你直接写出所有以格点为顶点，OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标．
（3）如图2，将△ABC绕顶点B按顺时针方向旋转60°，得到△DBE，连接AD、DC，∠DCB=30°．求证：DC²+BC²=AC²，即四边形ABCD是勾股四边形．
（4）若将图2中△ABC绕顶点B按顺时针方向旋转a度（0°＜a＜90°），得到△DBE，连接AD、DC，则∠DCB=（$\frac{1}{2}$α）°，四边形BECD是勾股四边形．

17．计算（-2）²⁰⁰²+（-2）²⁰⁰¹所得的正确结果是（　　）

2²⁰⁰¹

-2²⁰⁰¹

15．

如图，已知荷叶高出水面0.6m，一阵风吹来，荷叶紧贴水面，这时它偏离原来的水平距离为1.2m，求荷叶的高度．

a³•a²=a⁶

试题分类