题目内容
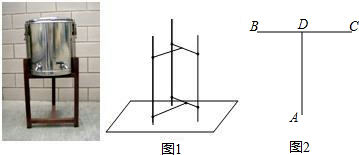
某中学在校内安放了几个圆柱形饮水桶的木制支架（如图1）．若不计木条的厚度，其俯视图如图2，已知AD垂直平分BC，AD=BC=40cm，则圆柱形饮水桶的底面半径的最大值是 cm．
考点：三角形的内切圆与内心
专题：应用题
分析：当圆柱形饮水桶的底面半径最大时，圆外接于△ABC；连接外心与B点，可通过勾股定理即可求出圆的半径．
解答：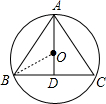
解：连接OB，如图，
当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大．
∵AD垂直平分BC，AD=BC=40cm，
∴O点在AD上，BD=20cm；
在Rt△0BD中，设半径为r，则OB=r，OD=40-r，
∴r2=（40-r）2+202，解得r=25．
即圆柱形饮水桶的底面半径的最大值为25cm．
故答案为25．
解：连接OB，如图，当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大．
∵AD垂直平分BC，AD=BC=40cm，
∴O点在AD上，BD=20cm；
在Rt△0BD中，设半径为r，则OB=r，OD=40-r，
∴r2=（40-r）2+202，解得r=25．
即圆柱形饮水桶的底面半径的最大值为25cm．
故答案为25．
点评：本题考查的是三角形的内切圆与内心，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
某反比例函数y=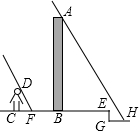
小强在周末搞了一次校外测量活动，他找到了一工厂的烟囱，正好阳光明媚，他就考虑用测量影子的方法去计算这个工厂烟囱的高度AB，但他发现烟囱的影子没有完全落在平地BE上，如图，影子一直落在了前面低洼处的H点，测得当时BE是22米，EG为1.6米，GH为8.4米（点C、F、B、E在和条水平线上，G、H在一条水平线上），他自己的身高CD是1.75米，当时他在阳光下的影长CF为1.6米，求这座烟囱AB的高度为多少米．（如果精确到0.1）下列命题是假命题的是（ ）
| A、两点之间，线段最短 |
| B、过不在同一直线上的三点有且只有一个圆 |
| C、一组对应边相等的两个等边三角形全等 |
| D、对角线相等的四边形是矩形 |
如图．AD是⊙O的直径，BC=CD，∠A=30°，求∠B的度数．若将抛物线C：y=2x2-4x+1向右平移3个单位得到抛物线C′则抛物线C与C′一定关于某条直线对称，这条直线是（ ）
A、x=
| ||
| B、x=2 | ||
C、x=
| ||
| D、x=3 |
如图，在△ABC中，∠B与∠C的平分线交于点O，过O点作DE∥BC，分别交AB，AC于点D，E．若AB=7，AC=6，则△ADE的周长是