题目内容
 如图所示,某住宅社区在相邻两楼之间修建一个上方是一个直径为4m的半圆,下方是一个宽为2.6m的长方形仿古通道,现有一辆卡车装满家具后,高3.9m,宽2.4m,请问这辆送家具的卡车能否通过这个通道?
如图所示,某住宅社区在相邻两楼之间修建一个上方是一个直径为4m的半圆,下方是一个宽为2.6m的长方形仿古通道,现有一辆卡车装满家具后,高3.9m,宽2.4m,请问这辆送家具的卡车能否通过这个通道?考点:垂径定理的应用,勾股定理
专题:
分析:先求出半圆的半径,再作EF∥AB,过点O作OD⊥EF于点D,使EF=2.4m,连接OF,根据勾股定理求出OD的长,进而可得出结论.
解答: 解:∵半圆的直径为4m,
解:∵半圆的直径为4m,
∴半径为2m.
作EF∥AB,过点O作OD⊥EF于点D,使EF=2.4m,连接OF,
∵EF=2.4m,
∴DF=1.2m,
∴OD=
=
=1.6m,
∴这辆送家具的卡车能通过这个通道.
 解:∵半圆的直径为4m,
解:∵半圆的直径为4m,∴半径为2m.
作EF∥AB,过点O作OD⊥EF于点D,使EF=2.4m,连接OF,
∵EF=2.4m,
∴DF=1.2m,
∴OD=
| OF2-DF2 |
| 22-1.22 |
∴这辆送家具的卡车能通过这个通道.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若将抛物线C:y=2x2-4x+1向右平移3个单位得到抛物线C′则抛物线C与C′一定关于某条直线对称,这条直线是( )
A、x=
| ||
| B、x=2 | ||
C、x=
| ||
| D、x=3 |
 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点
电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点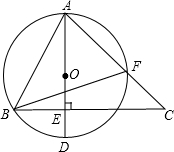 如图,AD是⊙O的直径,AB、AF是弦,BE⊥AD与AF的延长线交于点C.
如图,AD是⊙O的直径,AB、AF是弦,BE⊥AD与AF的延长线交于点C.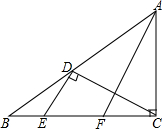 如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点.
如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点. 如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF. 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=