题目内容
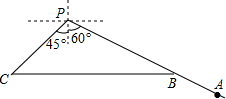 如图,甲船在港口P的南偏西60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向.求乙船的航行速度.(结果精确到个位,参考数据:
如图,甲船在港口P的南偏西60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向.求乙船的航行速度.(结果精确到个位,参考数据:| 2 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:作PD⊥BC于D,构造Rt△PCD和Rt△PBD,利用解直角三角形的方法求出PC的长,再求船的航行速度.
解答: 解:作PD⊥BC于D,
解:作PD⊥BC于D,
AB=5×2=10海里,PB=3010=20海里,
∵∠DPB=60°,
∴PD=PB•cos60°=20×
=10海里,
∵∠CPD=45°,
∴CP=
=
=10×
=10
海里,
10
÷2=5
≈5×1.414=7海里/时.
答:乙船的航行速度为7海里/时.
 解:作PD⊥BC于D,
解:作PD⊥BC于D,AB=5×2=10海里,PB=3010=20海里,
∵∠DPB=60°,
∴PD=PB•cos60°=20×
| 1 |
| 2 |
∵∠CPD=45°,
∴CP=
| PD |
| COS45° |
| 10 | ||||
|
| 2 | ||
|
| 2 |
10
| 2 |
| 2 |
答:乙船的航行速度为7海里/时.
点评:本题考查了解直角三角形的应用--方向角问题,构造直角三角形,灵活运用解直角三角形的方法是解题的关键.

练习册系列答案
相关题目
若将抛物线C:y=2x2-4x+1向右平移3个单位得到抛物线C′则抛物线C与C′一定关于某条直线对称,这条直线是( )
A、x=
| ||
| B、x=2 | ||
C、x=
| ||
| D、x=3 |
 某反比例函数y=
某反比例函数y=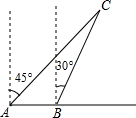 如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?
如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?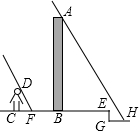 小强在周末搞了一次校外测量活动,他找到了一工厂的烟囱,正好阳光明媚,他就考虑用测量影子的方法去计算这个工厂烟囱的高度AB,但他发现烟囱的影子没有完全落在平地BE上,如图,影子一直落在了前面低洼处的H点,测得当时BE是22米,EG为1.6米,GH为8.4米(点C、F、B、E在和条水平线上,G、H在一条水平线上),他自己的身高CD是1.75米,当时他在阳光下的影长CF为1.6米,求这座烟囱AB的高度为多少米.(如果精确到0.1)
小强在周末搞了一次校外测量活动,他找到了一工厂的烟囱,正好阳光明媚,他就考虑用测量影子的方法去计算这个工厂烟囱的高度AB,但他发现烟囱的影子没有完全落在平地BE上,如图,影子一直落在了前面低洼处的H点,测得当时BE是22米,EG为1.6米,GH为8.4米(点C、F、B、E在和条水平线上,G、H在一条水平线上),他自己的身高CD是1.75米,当时他在阳光下的影长CF为1.6米,求这座烟囱AB的高度为多少米.(如果精确到0.1)