题目内容
8.在平面直角坐标系中,A(4,0),B(0,3),在x轴上取一点C,使以B,O,C为顶点的三角形与△AOB相似,写出符合请条件的C点坐标(-4,0)或($\frac{9}{4}$,0)或(-$\frac{9}{4}$,0).分析 以B、O、C为顶点的三角形与△AOB相似,两个三角形中O与O一定是对应顶点,C与△AOB中的A可能是对应顶点,也可能与B是对应顶点,应分两种情况进行讨论.
解答 解:∵A(4,0),B(0,3),
∴OA=4,OB=3,
∵在x轴上取一点C,使以B,O,C为顶点的三角形与△AOB相似,
∴分两种情况:如图所示:
①当C与A是对应顶点时,$\frac{OC}{OA}=\frac{OB}{OB}$=1,
∴OC=OA=4,
∴C点坐标为(-4,0);
②当C与B是对应顶点时,$\frac{OC}{OB}=\frac{OB}{OA}$,
即$\frac{OC}{3}=\frac{3}{4}$,
∴OC=$\frac{9}{4}$,
∴C点坐标为($\frac{9}{4}$,0)或(-$\frac{9}{4}$,0);
综上所述:符合请条件的C点坐标为(-4,0)或($\frac{9}{4}$,0)或(-$\frac{9}{4}$,0);
故答案为:(-4,0)或($\frac{9}{4}$,0)或(-$\frac{9}{4}$,0).
点评 本题主要考查了相似三角形的性质,根据对应顶点的情况讨论是解题关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.已知两点M(3,2),N(-1,3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( )
| A. | (0,$-\frac{7}{4}$) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{7}{5}$,0) |
3.下列各式变形正确的是( )
| A. | 如果2x=2y+1,那么x=y+1 | B. | 如果2=5+3x,那么3x=5-2 | ||
| C. | 如果x-3=y-3,那么x=y | D. | 如果-8x=4,那么x=-2 |
 如图,点O是数轴的原点,点A是数轴上的一个定点,点A表示的数为-15,点B在数轴上,且OB=3OA,数轴上的两个动点M,N分别从点A和点O同时出发,向右移动,点M的运动速度为每秒3个单位,点N的运动速度为每秒2个单位.
如图,点O是数轴的原点,点A是数轴上的一个定点,点A表示的数为-15,点B在数轴上,且OB=3OA,数轴上的两个动点M,N分别从点A和点O同时出发,向右移动,点M的运动速度为每秒3个单位,点N的运动速度为每秒2个单位.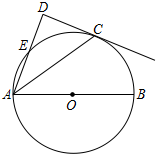 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E 如图所示,已知BE与CD相交于F,且∠B=∠C,∠1=∠2,求证:DF=EF.
如图所示,已知BE与CD相交于F,且∠B=∠C,∠1=∠2,求证:DF=EF.
 如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,
如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,