题目内容
12.从长度分别为x(x为正整数)、4、6、8的四条线段中任选三条作边,能构成三角形的概率为$\frac{1}{4}$,若长为x的线段在四条线段中最短,则x可取的值为1或2.分析 由从长度分别为x(x为正整数)、4、6、8的四条线段中任选三条作边,能构成三角形的概率为$\frac{1}{4}$,可得只有4,6,8能组成三角形,又由三角形的三边关系,求得x的值.
解答 解:∵从长度分别为x(x为正整数)、4、6、8的四条线段中任选三条作边,能构成三角形的概率为$\frac{1}{4}$,
∴只有4,6,8能组成三角形,
∵长为x的线段在四条线段中最短,
∴x+4≤6,
∵x为正整数,
∴x=1或2.
故答案为:1或2.
点评 此题考查了概率公式的应用以及三角形的三边关系.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
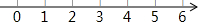 解不等式组$\left\{\begin{array}{l}{2x-1>x+1①}\\{4x≤3x+5②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{2x-1>x+1①}\\{4x≤3x+5②}\end{array}\right.$ 图甲是由若干个小正方体搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数,那么这个几何体的主视图是( )
图甲是由若干个小正方体搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数,那么这个几何体的主视图是( )



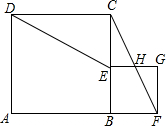 如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.
如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.