题目内容
6. 如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.(1)求证:BD=CE;
(2)连接BC,AO,并延长AO交BC于点F,试判断直线AF与BC的位置关系,并说明理由.
分析 (1)根据垂直定义求出∠ADC=∠AEB=90°,根据AAS推出△ABE≌△ACD,根据全等三角形的判定推出AD=AE,根据AB-AD=AC-AC,即可解答;
(2)求出∠ADC=∠AEB=90°,根据HL推出Rt△ADO≌Rt△AEO,根据全等三角形的性质推出∠DAO=∠EAO,根据等腰三角形的性质推出即可.
解答 解:(1)∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
$\left\{\begin{array}{l}{∠BAE=∠CAD}\\{∠AEB=∠ADC}\\{AB=AC}\end{array}\right.$
∴△ABE≌△ACD(AAS),
∴AD=AE,
∵AB=AC,
∴AB-AD=AE-AC,
即BD=CE.
(2)如图,
∵∠ADC=∠AEB=90°,
在Rt△ADO和Rt△AEO中,
$\left\{\begin{array}{l}{AO=AO}\\{AD=AE}\end{array}\right.$,
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∵AB=AC,
∴AF⊥BC.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,解此题的关键是求出△ABE≌△ACD和Rt△ADO≌Rt△AEO,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
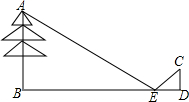 如图所示,在距树18米的地面上平放一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰巧看见树顶,若人眼C距地面1.4米.
如图所示,在距树18米的地面上平放一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰巧看见树顶,若人眼C距地面1.4米. 如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.
如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.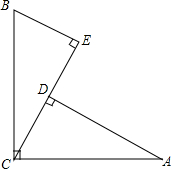 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.求证:
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.求证: 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.
如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.