题目内容
17. 如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.
如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.
分析 易证△AEB∽△ADC,可得AE:AB=AD;AC,即可证△ADE∽△ACB,即可求得DE的值.
解答 解:∵AE⊥BC,CD⊥AB,
∴∠AEB=∠BDC=90°,
∵∠B=∠B,
∴△AEB∽△BDC,
∴$\frac{BE}{AB}=\frac{BD}{BC}$,
∵∠B=∠B
∴△BDE∽△ACB,
∴$\frac{BD}{BC}=\frac{DE}{AC}$
∵∠B=45°,
在RT△ADC中,$\frac{BD}{BC}$=$\frac{\sqrt{2}}{2}$,
∴DE=2$\sqrt{2}$.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,在△ABC中,AB=AC,点D为BC上一点,点G为AD上一点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,求证:∠1=∠2.
如图,在△ABC中,AB=AC,点D为BC上一点,点G为AD上一点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,求证:∠1=∠2. 如图,在△ABC中,DE∥AC,EF∥AB,求证:∠EFC+∠FEC+∠DEB=180°.
如图,在△ABC中,DE∥AC,EF∥AB,求证:∠EFC+∠FEC+∠DEB=180°.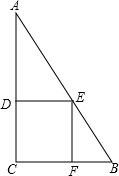 如图,在Rt△ABC中,AC=h cm,四边形DEFC是矩形,且点D、E、F在△ABC的边上,设AD=x cm,CF=$\frac{20x}{h}$cm,矩形DEFC的面积为y cm2.
如图,在Rt△ABC中,AC=h cm,四边形DEFC是矩形,且点D、E、F在△ABC的边上,设AD=x cm,CF=$\frac{20x}{h}$cm,矩形DEFC的面积为y cm2.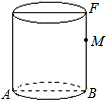 如图,已知圆柱体底面直径AB为2cm,高为4cm
如图,已知圆柱体底面直径AB为2cm,高为4cm  如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O. 如图,在Rt△ABC中,∠C=90°,∠BAC=2∠B,AD是∠BAC的平分线,请说明CD与BC的数量关系.
如图,在Rt△ABC中,∠C=90°,∠BAC=2∠B,AD是∠BAC的平分线,请说明CD与BC的数量关系.