题目内容
19.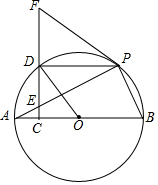 如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.
如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.(1)证明:FP是⊙O的切线;
(2)若四边形OBPD是菱形,证明:FD=ED.
分析 (1)连接OP,根据等腰三角形的性质得到∠A=∠APO,根据垂直的定义得到∠A+∠AEC=90°,等量代换得到∠AEC=∠FPE,于是得到OP⊥PF,根据切线的判定定理即可得到结论;
(2)根据菱形的性质得到PB=OB,推出△OPB是等边三角形,得到∠B=∠BOP=60°,于是得到△FPE是等边三角形,根据等边三角形的性质即可得到结论.
解答 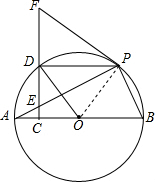 证明:(1)连接OP,
证明:(1)连接OP,
∵OP=OA,
∴∠A=∠APO,
∵EC⊥AB,
∴∠A+∠AEC=90°,
∵∠FPE=∠FEP,∠FEP=∠AEC,
∴∠AEC=∠FPE,
∴∠OPA+∠FPA=90°,
∴OP⊥PF,
∴FP是⊙O的切线;
(2)∵四边形OBPD是菱形,
∴PB=OB,
∵OB=OP,
∴OP=OB=PB,
∴△OPB是等边三角形,
∴∠B=∠BOP=60°,
∴∠A=30°,
∴∠AEC=∠FEP=60°,
∴∠FPE=∠FEP=60°,
∴△FPE是等边三角形,
∵PD∥AB,
∴PD⊥EF,
∴FD=ED.
点评 本题考查了切线的判定,菱形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
9.下列计算正确的是( )
| A. | x6+x6=x12 | B. | (x2)3=x5 | C. | x-1=x | D. | x2•x3=x5 |
4.若分式-$\frac{1}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x=2 | D. | x<2 |
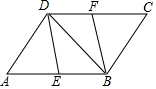 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.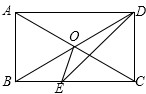 如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE. 如图,在△ABC中,∠ACB=90°,CD⊥AB于D点,AB=5,CD=2,则△ABC的周长是3$\sqrt{5}$+5.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D点,AB=5,CD=2,则△ABC的周长是3$\sqrt{5}$+5.