题目内容
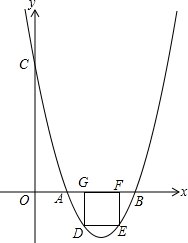 如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.
如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.(1)求点C的坐标;
(2)求抛物线的解析式及其对称轴;
(3)若正方形DEFG内接于抛物线和x轴(边FG在x轴上,点D,E分别在抛物线上),求S正方形DEFG.
考点:二次函数的性质,二次函数图象上点的坐标特征,待定系数法求二次函数解析式
专题:
分析:(1)由A(2,0),B(6,0),可得AB=6-2=4.由S△ABC=16,根据三角形的面积公式得出
×4•OC=16,求出OC=8,于是得到点C的坐标为(0,8);
(2)由抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),可设抛物线的解析式为y=a(x-2)(x-6),再将C(0,8)代入,利用待定系数法求出抛物线的解析式为y=
x2-
x+8,进而得到对称轴为直线x=4;
(3)设正方形DEFG的边长为m,则m>0,根据题意得出D(4-
m,-m),E(4+
m,-m).将E(4+
m,-m)代入y=
x2-
x+8,得-m=
×(4+
m)2-
×(4+
m)+8,解方程求出m的值,进而得到S正方形DEFG.
| 1 |
| 2 |
(2)由抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),可设抛物线的解析式为y=a(x-2)(x-6),再将C(0,8)代入,利用待定系数法求出抛物线的解析式为y=
| 2 |
| 3 |
| 16 |
| 3 |
(3)设正方形DEFG的边长为m,则m>0,根据题意得出D(4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
| 1 |
| 2 |
解答:解:(1)∵A(2,0),B(6,0),
∴AB=6-2=4.
∵S△ABC=16,
∴
×4•OC=16,
∴OC=8,
∴点C的坐标为(0,8);
(2)∵抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),
∴可设抛物线的解析式为y=a(x-2)(x-6),
将C(0,8)代入,得8=12a,
解得a=
,
∴y=
(x-2)(x-6)=
x2-
x+8,
故抛物线的解析式为y=
x2-
x+8,其对称轴为直线x=4;
(3)设正方形DEFG的边长为m,则m>0,
∵正方形DEFG内接于抛物线和x轴(边FG在x轴上,点D,E分别在抛物线上),
∴D(4-
m,-m),E(4+
m,-m).
将E(4+
m,-m)代入y=
x2-
x+8,
得-m=
×(4+
m)2-
×(4+
m)+8,
整理得,m2+6m-16=0,
解得m1=2,m2=-8(不合题意舍去),
∴正方形DEFG的边长为2,
∴S正方形DEFG=22=4.
∴AB=6-2=4.
∵S△ABC=16,
∴
| 1 |
| 2 |
∴OC=8,
∴点C的坐标为(0,8);
(2)∵抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),
∴可设抛物线的解析式为y=a(x-2)(x-6),
将C(0,8)代入,得8=12a,
解得a=
| 2 |
| 3 |
∴y=
| 2 |
| 3 |
| 2 |
| 3 |
| 16 |
| 3 |
故抛物线的解析式为y=
| 2 |
| 3 |
| 16 |
| 3 |
(3)设正方形DEFG的边长为m,则m>0,
∵正方形DEFG内接于抛物线和x轴(边FG在x轴上,点D,E分别在抛物线上),
∴D(4-
| 1 |
| 2 |
| 1 |
| 2 |
将E(4+
| 1 |
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
得-m=
| 2 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
| 1 |
| 2 |
整理得,m2+6m-16=0,
解得m1=2,m2=-8(不合题意舍去),
∴正方形DEFG的边长为2,
∴S正方形DEFG=22=4.
点评:本题考查了待定系数法求二次函数解析式,三角形的面积,二次函数的性质,二次函数图象上点的坐标特征,正方形的性质,难度适中.(3)中设出正方形DEFG的边长为m,根据二次函数与正方形的性质用含m的代数式正确表示点D与点E的坐标是解题的关键.

练习册系列答案
相关题目
直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则r的取值范围是( )
| A、r<5 | B、r=5 |
| C、r>5 | D、r≥5 |
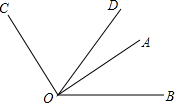 如图,已知∠AOB=40°,∠AOC=90°,OD平分∠BOC,则∠AOD的度数是( )
如图,已知∠AOB=40°,∠AOC=90°,OD平分∠BOC,则∠AOD的度数是( )| A、20° | B、25° |
| C、30° | D、35° |
 如图,直线a、b被三条互相平行的直线l1,l2,l3所截,AB=3,BC=2,则DE:DF=( )
如图,直线a、b被三条互相平行的直线l1,l2,l3所截,AB=3,BC=2,则DE:DF=( )| A、2:3 | B、3:2 |
| C、2:5 | D、3:5 |
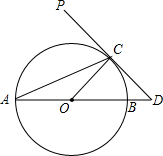 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.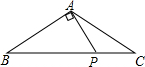 已知,如图,△ABC中,AB=AC,∠BAC=120°,P是BC上的点且PA⊥AB,求证:AP=PC.
已知,如图,△ABC中,AB=AC,∠BAC=120°,P是BC上的点且PA⊥AB,求证:AP=PC.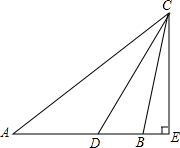 如图,△ABC中,AB=BC,CD平分∠ACB,CE⊥AB于E,若∠DCE=30°,求△ABC各角的度数.
如图,△ABC中,AB=BC,CD平分∠ACB,CE⊥AB于E,若∠DCE=30°,求△ABC各角的度数.