题目内容
20.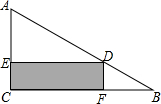 如图,在Rt△ABC的内部作一个矩形CEDF,其中CE、CF在三角形的边AC、BC上,已知AC=6cm,BC=8cm.设长方形的面积为y m2,边长DE=x m.
如图,在Rt△ABC的内部作一个矩形CEDF,其中CE、CF在三角形的边AC、BC上,已知AC=6cm,BC=8cm.设长方形的面积为y m2,边长DE=x m.(1)求y与x的函数关系式,写出x的取值范围;
(2)画出函数的图象;
(3)根据图象,判断当x为何值时,y的值最大?最大值是多少?
分析 (1)先证明△AED∽△ACB,得到$\frac{AE}{AC}=\frac{ED}{CB}$,可求得AE=$\frac{3}{4}x$,所以EC=6-$\frac{3}{4}x$,然后根据矩形的面积公式求得y与x的函数关系式即可.
(2)根据函数关系式求得抛物线与x轴两交点的坐标,然后再求得抛物线的顶点坐标,即可画出函数的图象;
(3)根据顶点坐标为(4,9)可求得当x=4时,最大值为y=9.
解答 解:(1)∵四边形ECFD是矩形,
∴ED∥BC.
∴△AED∽△ACB.
∴$\frac{AE}{AC}=\frac{ED}{CB}$,即$\frac{AE}{6}=\frac{x}{8}$.
∴AE=$\frac{3}{4}x$.
∴EC=6-$\frac{3}{4}x$.
∴y=(6-$\frac{3}{4}x$)x=$-\frac{3}{4}{x}^{2}+6x$.
∴y与x的函数关系式为y=$-\frac{3}{4}{x}^{2}+6x$(0<x<8).
(2)令y=0得;y=$-\frac{3}{4}{x}^{2}+6x$=0,
解得:x1=0,x2=8.
∴顶点的横坐标为4,将x=4代入得y=12.
∴抛物线的顶点坐标为(4,12)
过点(0,0)、(8,0)、(4,12)画出函数图形如图所示: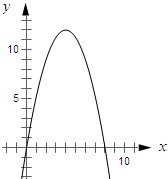
(3)∵a<0,
∴抛物线有最大值.
由(2)可知:抛物线的顶点坐标为(4,12),
∴当x=4时,有最大值,最大值为12.
点评 本题主要考查的是二次函数的图象和性质,利用二次函数的图象和性质,确定出函数的点坐标以及与x的交点坐标是解题的关键.

练习册系列答案
相关题目
11. 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A. | 中 | B. | 国 | C. | 的 | D. | 梦 |
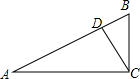 如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.
如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.
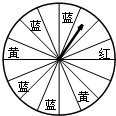 如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.