题目内容
12.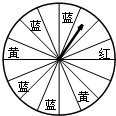 如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.(1)分别计算获一、二、三等奖的概率.
(2)老李一次性购物满了300元,摇奖一次,获奖的概率是多少?请你预测一下老李摇奖结果会有哪几种情况?
分析 (1)找到红色区域的份数占总份数的多少即为获得一等奖的概率;找到黄色和蓝色区域的份数占总份数的多少即为获得二、三等奖的概率.
(2)用有颜色的区域数除以所有扇形的个数即可求得中奖的概率.
解答 解:(1)整个圆周被分成了16份,红色为1份,
∴获得一等奖的概率为:$\frac{1}{16}$;
整个圆周被分成了16份,黄色为2份,
∴获得二等奖的概率为:$\frac{2}{16}$=$\frac{1}{8}$;
整个圆周被分成了16份,蓝色为4份,
∴获得三等奖的概率为$\frac{4}{16}$=$\frac{1}{4}$;
(2)∵共分成了16份,其中有奖的有1+2+4=7份,
∴P(获奖)=$\frac{7}{16}$;
老李摇奖共有四种结果,一等奖、二等奖、三等奖、不中奖.
点评 此题考查了概率公式的应用.注意用到的知识点为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,难度适中..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在利用太阳能热水器来加热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,这个问题中因变量是( )
| A. | 水的温度 | B. | 太阳光强弱 | C. | 太阳照射时间 | D. | 热水器的容积 |
17. 已知,∠AOB=30°,点M1,M2,M3…在射线OB上,点N1,N2,N3…在射线0A上,△M1N1M2,△M2N2M3,△M3N3M4…均为等边三角形.若OM1=1,则△MnNnMn+1的边长为( )
已知,∠AOB=30°,点M1,M2,M3…在射线OB上,点N1,N2,N3…在射线0A上,△M1N1M2,△M2N2M3,△M3N3M4…均为等边三角形.若OM1=1,则△MnNnMn+1的边长为( )
 已知,∠AOB=30°,点M1,M2,M3…在射线OB上,点N1,N2,N3…在射线0A上,△M1N1M2,△M2N2M3,△M3N3M4…均为等边三角形.若OM1=1,则△MnNnMn+1的边长为( )
已知,∠AOB=30°,点M1,M2,M3…在射线OB上,点N1,N2,N3…在射线0A上,△M1N1M2,△M2N2M3,△M3N3M4…均为等边三角形.若OM1=1,则△MnNnMn+1的边长为( )| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 2n |
4.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=2 | C. | $\sqrt{6}$×$\sqrt{2}$=2$\sqrt{3}$ | D. | $\sqrt{6}$÷$\sqrt{2}$=3 |
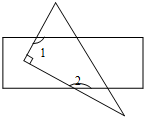 如图,将一张长方形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的度数是270°.
如图,将一张长方形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的度数是270°.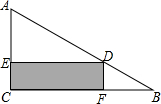 如图,在Rt△ABC的内部作一个矩形CEDF,其中CE、CF在三角形的边AC、BC上,已知AC=6cm,BC=8cm.设长方形的面积为y m2,边长DE=x m.
如图,在Rt△ABC的内部作一个矩形CEDF,其中CE、CF在三角形的边AC、BC上,已知AC=6cm,BC=8cm.设长方形的面积为y m2,边长DE=x m.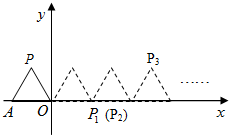 如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…P2015的位置,则点P2015的横坐标为2014.
如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…P2015的位置,则点P2015的横坐标为2014.