题目内容
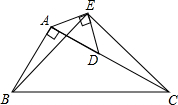 如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.下列判断正确的有( )
①△ABE≌△DCE;②BE=EC;③BE⊥EC;④EC=
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,等腰直角三角形
专题:压轴题
分析:根据AC=2AB,点D是AC的中点求出AB=CD,再根据△ADE是等腰直角三角形求出AE=DE,并求出∠BAE=∠CDE=135°,然后利用“边角边”证明△ABE和△DCE全等,从而判断出①小题正确;根据全等三角形对应边相等可得BE=EC,从而判断出②小题正确;根据全等三角形对应角相等可得∠AEB=∠DEC,然后推出∠BEC=∠AED,从而判断出③小题正确;根据等腰直角三角形斜边等于直角边的
倍,用DE表示出AD,然后得到AB、AC,再根据勾股定理用DE与EC表示出BC,整理即可得解,从而判断出④小题正确.
| 2 |
解答:解:∵AC=2AB,点D是AC的中点,
∴CD=
AC=AB,
∵△ADE是等腰直角三角形,
∴AE=DE,
∠BAE=90°+45°=135°,∠CDE=180°-45°=135°,
∴∠BAE=∠CDE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),故①小题正确;
∴BE=EC,∠AEB=∠DEC,故②小题正确;
∵∠AEB+∠BED=90°,
∴∠DEC+∠BED=90°,
∴BE⊥EC,故③小题正确;
∵△ADE是等腰直角三角形,
∴AD=
DE,
∵AC=2AB,点D是AC的中点,
∴AB=
DE,AC=2
DE,
在Rt△ABC中,BC2=AB2+AC2=(
DE)2+(2
DE)2=10DE2,
∵BE=EC,BE⊥EC,
∴BC2=BE2+EC2=2EC2,
∴2EC2=10DE2,
解得EC=
DE,故④小题正确,
综上所述,判断正确的有①②③④共4个.
故选D.
∴CD=
| 1 |
| 2 |
∵△ADE是等腰直角三角形,
∴AE=DE,
∠BAE=90°+45°=135°,∠CDE=180°-45°=135°,
∴∠BAE=∠CDE,
在△ABE和△DCE中,
|
∴△ABE≌△DCE(SAS),故①小题正确;
∴BE=EC,∠AEB=∠DEC,故②小题正确;
∵∠AEB+∠BED=90°,
∴∠DEC+∠BED=90°,
∴BE⊥EC,故③小题正确;
∵△ADE是等腰直角三角形,
∴AD=
| 2 |
∵AC=2AB,点D是AC的中点,
∴AB=
| 2 |
| 2 |
在Rt△ABC中,BC2=AB2+AC2=(
| 2 |
| 2 |
∵BE=EC,BE⊥EC,
∴BC2=BE2+EC2=2EC2,
∴2EC2=10DE2,
解得EC=
| 5 |
综上所述,判断正确的有①②③④共4个.
故选D.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,准确识图,根据△ADE是等腰直角三角形推出AE=DE,∠BAE=∠CDE=135°是解题的关键,也是解决本题的突破口.

练习册系列答案
相关题目
 如图,等边三角形ABC内有一个正方形DEFG,已知等边三角形边长为3,则正方形的边长为
如图,等边三角形ABC内有一个正方形DEFG,已知等边三角形边长为3,则正方形的边长为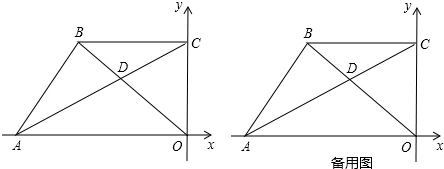
 已知梯形ABCD中,AD∥EF∥GH∥BC,AE:EG:GB=1:2:3,AD=3,BC=9,则EF+GH=( )
已知梯形ABCD中,AD∥EF∥GH∥BC,AE:EG:GB=1:2:3,AD=3,BC=9,则EF+GH=( )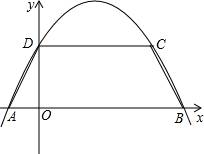 如图,抛物线y=ax2-3ax+b经过A(-1,0),C(3,2)两点,与y轴交于点D,与x轴交于A、B.
如图,抛物线y=ax2-3ax+b经过A(-1,0),C(3,2)两点,与y轴交于点D,与x轴交于A、B.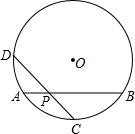 如图,在半径为6的⊙O中,弦AB的长为
如图,在半径为6的⊙O中,弦AB的长为