题目内容
 如图,等边三角形ABC内有一个正方形DEFG,已知等边三角形边长为3,则正方形的边长为
如图,等边三角形ABC内有一个正方形DEFG,已知等边三角形边长为3,则正方形的边长为考点:等边三角形的性质,正方形的性质
专题:计算题
分析:过A作AM垂直于BC,交BC于M点,交DG于N点,由四边形DEFG为正方形,得到DG与BC平行,且四条边相等,设正方形的边长为x,由两直线平行得到两对同位角相等,利用两对角相等的三角形相似可得出三角形ADG与三角形ABC相似,由相似得比例,将各自的值代入列出关于x的方程,求出方程的解得到x的值,即为正方形的边长.
解答:解:过A作AM⊥BC,交BC于M,交DG于N,如图所示:

∵四边形DEFG为正方形,
∴DG∥BC,DE=EF=FG=DG,
∴∠ADG=∠B,∠AGD=∠C,AN⊥DG,
∴△ADG∽△ABC,
设DE=EF=FG=DG=x,
又△ABC为边长为3的等边三角形,AM⊥BC,
∴M为BC的中点,即BM=CM=
BC=
,
在Rt△ABM中,根据勾股定理得:AM=
=
,
∴
=
,即
=
,
解得:x=6
-9,
则正方形的边长为6
-9.
故答案为:6
-9

∵四边形DEFG为正方形,
∴DG∥BC,DE=EF=FG=DG,
∴∠ADG=∠B,∠AGD=∠C,AN⊥DG,
∴△ADG∽△ABC,
设DE=EF=FG=DG=x,
又△ABC为边长为3的等边三角形,AM⊥BC,
∴M为BC的中点,即BM=CM=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△ABM中,根据勾股定理得:AM=
| AB2-BM2 |
3
| ||
| 2 |
∴
| DG |
| BC |
| AN |
| AM |
| x |
| 3 |
| ||||
|
解得:x=6
| 3 |
则正方形的边长为6
| 3 |
故答案为:6
| 3 |
点评:此题考查了等边三角形的性质,相似三角形的判定与性质,勾股定理,平行线的性质,以及正方形的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将正偶数按下表排成5列
根据上面排列的规律,2012应排在( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … |
| A、第502行第1列 |
| B、第250行第5列 |
| C、第251行第4列 |
| D、第252行第3列 |
 如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC,若△ABC的面积为1,S△AEF=2S△EBC,则S△CEF为
如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC,若△ABC的面积为1,S△AEF=2S△EBC,则S△CEF为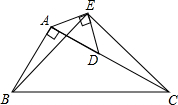 如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.