题目内容
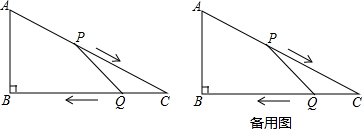
1.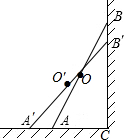 如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.
如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.
分析 根据直角三角形斜边上的中线等于斜边的一半确定∠OCO′的度数,根据弧长公式求出梯子AB的中点O划过的路程.
解答  解:∵∠ACB=90°,O为AB的中点,
解:∵∠ACB=90°,O为AB的中点,
∴CO=OB,
∴∠OCB=∠CBA=20°,
∵∠CB′A′=30°,
∴∠CA′B′=60°
∵∠ACB=90°,O′为A′B′的中点,
∴CO′=O′A′,
∴∠O′CA′=∠CA′B′=60°,
∴∠OCO′=10°,
故梯子AB的中点O划过的路程$\widehat{OO′}$为:$\frac{10×π×3}{180}$=$\frac{1}{6}$π.
点评 本题考查的是直角三角形的性质、圆的轨迹和弧长的计算,掌握直角三角形斜边上的中线等于斜边的一半、确定梯子AB的中点O划过的轨迹、正确运用弧长公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各式中,运算结果等于x2-4x-12的是( )
| A. | (x+3)(x-4) | B. | (x-2)(x+6) | C. | (x-3)(x+4) | D. | (x+2)(x-6) |
 如图所示,面积为400m2的正方形的四个角是面积为3m2的小正方形.求a的值.
如图所示,面积为400m2的正方形的四个角是面积为3m2的小正方形.求a的值.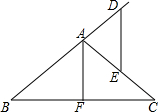 如图,在△ABC中,AB=AC,AF⊥BC,点D在BA的延长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,并证明你的结论.
如图,在△ABC中,AB=AC,AF⊥BC,点D在BA的延长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,并证明你的结论.