题目内容
16.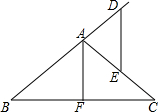 如图,在△ABC中,AB=AC,AF⊥BC,点D在BA的延长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,并证明你的结论.
如图,在△ABC中,AB=AC,AF⊥BC,点D在BA的延长线上,点E在AC上,且AD=AE,试探索DE与AF的位置关系,并证明你的结论.
分析 根据等腰三角形的性质三线合一得到∠FAC=$\frac{1}{2}$∠BAC,根据外角的性质得到∠BAC=∠ADE+∠AED,由于AD=AE,于是得到∠AED=∠ADE,等量代换得到∠FAC=∠AED,于是结论即可得出.
解答 解:DE∥AF,
理由:∵AB=AC,AF⊥BC,
∴∠FAC=$\frac{1}{2}$∠BAC,
∵∠BAC=∠ADE+∠AED,
∵AD=AE,
∴∠AED=∠ADE,
∴$∠AED=\frac{1}{2}∠$BAC,
∴∠FAC=∠AED,
∴AF∥DE.
点评 本题考查了等腰三角形的性质,平行线的判定,三角形的外角的性质,熟练掌握各定理是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
16.下列各式中,相等关系成立的是( )
| A. | xm+mn=xm+n | B. | xm•x-n=xm-n | C. | x3•x3=2x3 | D. | x6÷x2=x3 |
 如图,△ABC的高AD,BE相交于点F.
如图,△ABC的高AD,BE相交于点F.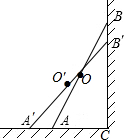 如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.
如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.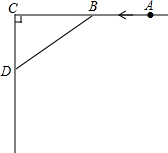 如图,AC⊥CD,甲、乙两人分别骑自行车从相距10km的A,C两地同时出发,各沿箭头所指方向前进.已知甲的速度是16km/h,乙的速度是12km/h,且当甲到达C地时两人停止运动.问:出发多少时间后两人相距最近?最近距离为多少千米?
如图,AC⊥CD,甲、乙两人分别骑自行车从相距10km的A,C两地同时出发,各沿箭头所指方向前进.已知甲的速度是16km/h,乙的速度是12km/h,且当甲到达C地时两人停止运动.问:出发多少时间后两人相距最近?最近距离为多少千米?