题目内容
3.如图,在△ABC中,∠B=90°,AB=6,BC=8,动点P从A点出发,沿AC向点C移动,速度为每秒2个单位长度,同时,动点Q从C点出发,沿CB向点B移动,速度为每秒1个单位长度,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.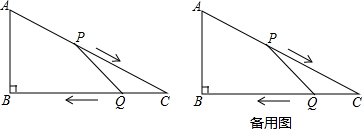
(1)当t=2.5秒时,求△CPQ的面积;
(2)求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;
(2)在P、Q移动的过程中,当t为何值时,△CPQ是等腰三角形?
分析 (1)首先利用勾股定理求得AC的长,然后过点P作PD⊥BC于D,利用三角形中位线定理即可求得PD的长;
(2)过点Q,作QE⊥PC于点E,易知Rt△QEC∽Rt△ABC,从而可求得QE的长,然后利用三角形的面积公式即可求解;
(2)PC=QC PQ=QC PC=PQ三种情况进行讨论求解即可.
解答 解:(1)如图1,过点P,作PD⊥BC于D.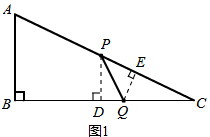
在Rt△ABC中,AB=6米,BC=8米,
由勾股定理得:AC$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{6}^{2}+{8}^{2}}$=10米
由题意得:AP=2t,则CQ=t,则PC=10-2t
∵t=2.5秒时,AP=2×2.5=5米,QC=2.5米
∴PD=$\frac{1}{2}$AB=3米.
∴S=$\frac{1}{2}$QC•PD=3.75平方米;
(2)如图1过点Q,作QE⊥PC于点E,
∵∠C=∠C,∠QEC=∠ABC,
∴Rt△QEC∽Rt△ABC.
∴$\frac{QE}{QC}=\frac{AB}{AC}$.
解得:QE=$\frac{3t}{5}$,
∴S=$\frac{1}{2}$PC•QE=$\frac{1}{2}$(10-2t)•$\frac{3t}{5}$=-$\frac{3}{5}$t2+3t(0<t<5)
(3)①当PC=QC时,PC=10-2t,QC=t,即10-2t=t,解得t=$\frac{10}{3}$秒;
②当PQ=CQ时,如图1,过点Q作QE⊥AC,则CE=$\frac{10-2t}{2}$=5-t,CQ=t,
由(2)可知△CEQ∽△CBA,故 $\frac{CE}{BC}=\frac{QC}{AC}$,即 $\frac{5-t}{8}=\frac{t}{10}$,解得t=$\frac{25}{9}$秒;
③当PC=PQ时,如图2,过点P作PE⊥BC.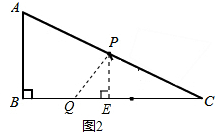
∵PQ=PC,PE⊥QC,
∴EC=$\frac{1}{2}QC$.
∴CE=$\frac{t}{2}$.
∵PE⊥QC,
∴∠PEC=90°.
∴∠PEC=∠ABC.
∵∠C=∠C,∠PEC=∠ABC,
∴△PCE∽△ACB.
∴$\frac{CE}{BC}=\frac{PC}{AC}$,即$\frac{t}{16}$=$\frac{10-2t}{10}$,解得t=$\frac{80}{21}$秒.
点评 本题主要考查了相似三角形的性质,以及圆和圆的位置关系,正确把图形之间的位置关系转化为线段之间的相等关系是解题的关键.

| A. | x≠2 | B. | x≠2且x≠4 | C. | x≠3且x≠4 | D. | x≠2,x≠3且x≠4 |
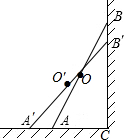 如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.
如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.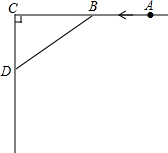 如图,AC⊥CD,甲、乙两人分别骑自行车从相距10km的A,C两地同时出发,各沿箭头所指方向前进.已知甲的速度是16km/h,乙的速度是12km/h,且当甲到达C地时两人停止运动.问:出发多少时间后两人相距最近?最近距离为多少千米?
如图,AC⊥CD,甲、乙两人分别骑自行车从相距10km的A,C两地同时出发,各沿箭头所指方向前进.已知甲的速度是16km/h,乙的速度是12km/h,且当甲到达C地时两人停止运动.问:出发多少时间后两人相距最近?最近距离为多少千米?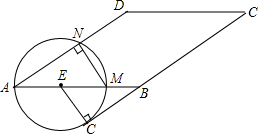 如图,在?ABCD(AB>AD)中,点E在边AB上,以点E为圆心,AE长为半径的⊙E分别交AB、AD于点N、N,与BC所在的直线相切于点G
如图,在?ABCD(AB>AD)中,点E在边AB上,以点E为圆心,AE长为半径的⊙E分别交AB、AD于点N、N,与BC所在的直线相切于点G