题目内容
6. 如图,对称轴为x=1的抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于C点,其中A点坐标为(-1,0)设抛物线的顶点为D.
如图,对称轴为x=1的抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于C点,其中A点坐标为(-1,0)设抛物线的顶点为D.(1)求抛物线的解析式及顶点坐标;
(2)M为x轴上的一点,当△MCD的周长最小时,求点M的坐标及△MCD的周长.
分析 解:(1)根据题意得出方程组,求出b和c的值,得出抛物线的解析式,即可求出顶点坐标;
(2)求出C(0,3),得出C点关于x轴的对称点C′(0,-3),连接C′D交x轴于M,则△MCD的周长最小,由待定系数法求出直线C′D的解析式,即可得出M($\frac{3}{7}$,0),过D作DE⊥y轴于E,得出DE=1,CD=1,C′E=7,由勾股定理求出CD=$\sqrt{2}$,C′D=5$\sqrt{2}$,即可得出△MCD的周长最小值.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{-\frac{b}{2×(-1)}=1}\\{-1-b+c=0}\end{array}\right.$,
解得:b=2,c=3,
∴抛物线的解析式为y═-x2+2x+3,
当x=1时,y=-1+2+3=4, ∴顶点D(1,4);
∴顶点D(1,4);
(2)当x=0时,y=3,
∴C(0,3),
∴C点关于x轴的对称点C′(0,-3),
连接C′D交x轴于M,则△MCD的周长最小,CM=C′M,
设直线C′D的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{k+b=4}\\{b=-3}\end{array}\right.$,
∴k=7,
∴y=7x-3,
当y=0时,7x-3=0,
解得:x=$\frac{3}{7}$,
∴M($\frac{3}{7}$,0),
过D作DE⊥y轴于E,
∵C(0,3),D(1,4),
∴DE=1,CD=1,C′E=7,
∴CD=$\sqrt{2}$,C′D=5$\sqrt{2}$,
∴△MCD的周长最小值=$\sqrt{2}$+5$\sqrt{2}$=6$\sqrt{2}$.
点评 本题考查了抛物线解析式的求法、轴对称的性质、勾股定理以及最小值问题;由待定系数法求出抛物线的解析式是解决问题的关键.

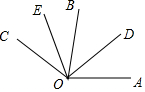 如图,OD平分∠AOB,OE平分∠BOC,若∠COD=100°,∠AOE=110°,则∠DOE=70°.
如图,OD平分∠AOB,OE平分∠BOC,若∠COD=100°,∠AOE=110°,则∠DOE=70°.
 如图,已知AC=BD,AF∥DE,请你添一个条件,∠ACF=∠DBE,使△AFC≌△DEB.
如图,已知AC=BD,AF∥DE,请你添一个条件,∠ACF=∠DBE,使△AFC≌△DEB.