题目内容
8.观察下面的几个算式:①16×14=224=1×(1+1)×100+6×4;
②23×27=621=2×(2+1)×100+3×7;
③32×38=1216=3×(3+1)×100+2×8.
…
(1)仿照上面的书写格式,请写出81×89的结果;
(2)利用多项式的乘法验证你所发现的规律(提示:可设这两个两位数分别是(10n+a),(10n+b),其中a+b=10)
分析 (1)观察上面几个式子,发现:左边两个因数的十位数字相同,个位数字和是10;则右边的结果是一个四位数,其中个位和十位上的数是左边两个因数的个位相乘,百位和千位上的数是左边十位上的数字和大于十位数字1的数相乘.根据这一规律即可写出81×89=7209;
(2)归纳总结得到的规律用n,a及b表示出来,左右两边化简后可得出左右两边相等,得证.
解答 解:(1)∵16×14=224=1×(1+1)×100+6×4;
23×27=621=2×(2+1)×100+3×7;
32×38=1216=3×(3+1)×100+2×8;
…,
∴81×89=8×(8+1)×100+1×9=7209;
(2)发现的规律为:(10n+a)•(10n+b)=100n(n+1)+ab,
∵a+b=10,
∴等式左边=100n2+10bn+10an+ab=100n2+10n(a+b)+ab=100n2+100n+ab,
右边=100n2+100n+ab,
∴左边=右边,
则(10n+a)•(10n+b)=100n(n+1)+ab.
点评 此题主要考查了整式混合运算的应用,找出题中的规律是解本题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
4.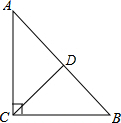 如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
 如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.下列说法中正确的有( )
①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个全等的位似图形的位似中心在两个图形之间或在这两个图形的公共边上;
④全等图形一定是位似图形,且位似比为1:1;
⑤若图形a与图形b是位似图形,图形b与图形c是位似图形,则图形a与图形c也一定是位似图形.
①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个全等的位似图形的位似中心在两个图形之间或在这两个图形的公共边上;
④全等图形一定是位似图形,且位似比为1:1;
⑤若图形a与图形b是位似图形,图形b与图形c是位似图形,则图形a与图形c也一定是位似图形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.关于x的方程x2-2x+m2-4=0的两个根互为倒数,则m的值为( )
| A. | $-\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $±\sqrt{5}$ | D. | ±2 |
 已知:如图所示,AB=AC,CE=BD,点D、E分别在AB、AC上.
已知:如图所示,AB=AC,CE=BD,点D、E分别在AB、AC上.