题目内容
已知抛物线y=ax2+bx+c与y=
x2的图象形状相同,开口方向也相同,且顶点坐标为(-2,-4).
(1)求函数解析式;
(2)求抛物线与x轴的两个交点A、B(A在B的左侧)及与y轴交点C构成的三角形面积.
| 1 |
| 4 |
(1)求函数解析式;
(2)求抛物线与x轴的两个交点A、B(A在B的左侧)及与y轴交点C构成的三角形面积.
考点:待定系数法求二次函数解析式,抛物线与x轴的交点
专题:计算题
分析:(1)由于已知顶点坐标,则可设顶点式,加上a=
,可直接得到所求抛物线解析式为y=
(x+2)2-4;
(2)根据坐标轴上点的坐标特征先分别求出A、B、C点的坐标,然后根据三角形面积公式求解.
| 1 |
| 4 |
| 1 |
| 4 |
(2)根据坐标轴上点的坐标特征先分别求出A、B、C点的坐标,然后根据三角形面积公式求解.
解答:解:(1)根据题意得,所求抛物线解析式为y=
(x+2)2-4=
x2+x-3;
(2)当x=0时,y=
x2+x-3=-3,则C点坐标为(0,-3);、
当y=0时,
(x+2)2-4=0,解得x1=-6,x2=2,则A(-6,0),B(2,0),
所以△ABC的面积=
×3×(2+6)=12.
| 1 |
| 4 |
| 1 |
| 4 |
(2)当x=0时,y=
| 1 |
| 4 |
当y=0时,
| 1 |
| 4 |
所以△ABC的面积=
| 1 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
-
的倒数是( )
| 1 |
| 3 |
| A、-3 | ||
B、-
| ||
C、
| ||
| D、3 |
下列抛物线中,与y=-
x2+3x-5的开口方向大小相同,只是位置不同的是( )
| 1 |
| 2 |
A、y=-
| ||||||
| B、y=-x2+x-5 | ||||||
C、y=-
| ||||||
D、y=-
|
用反证法证明“若⊙O的半径为r,点P到圆心的距离d<r,则点P在⊙O的内部”首先应假设( )
| A、d≤r |
| B、d≥r |
| C、点P在⊙O的外部 |
| D、点P在⊙O上或点P在⊙O的外部 |
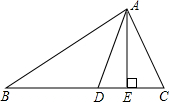 如图,AE,AD分别是△ABC的高和角平分线,且∠B=40°,∠C=60°,求∠BAD和∠DAE的度数.
如图,AE,AD分别是△ABC的高和角平分线,且∠B=40°,∠C=60°,求∠BAD和∠DAE的度数.