题目内容
19.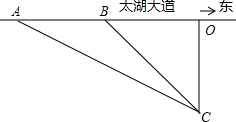 某同学为了检测车速,设计如下方案如图,观测点C选在东西方向的太湖大道上O点正南方向120米处.这时,一辆小轿车沿太湖大道由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为3秒,且∠ACO=60°,∠BCO=45°
某同学为了检测车速,设计如下方案如图,观测点C选在东西方向的太湖大道上O点正南方向120米处.这时,一辆小轿车沿太湖大道由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为3秒,且∠ACO=60°,∠BCO=45°(1)求AB的长;
(2)请判断此车是否超过了太湖大道每小时80千米的限制速度?
(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 (1)根据题意可以分别求得AO和BO的长,从而可以求得AB的长;
(2)根据题意可以求得此车的速度,从而可以判断此时是否超过了太湖大道每小时80千米的限制速度.
解答 解:(1)由题意可得,
CO=120米,∠COB=∠COA=90°,∠ACO=60°,∠BCO=45°,
∴AO=CO•tan60°=120$\sqrt{3}$米,BO=CO•tan45°=120×1=120米,
∴AB=AO-BO=(120$\sqrt{3}-120$)米,
即AB的长是(120$\sqrt{3}-120$)米;
(2)∵$\frac{120\sqrt{3}-120}{3}≈\frac{120×1.73-120}{3}$=29.2m/s=105.12千米/时>80千米/时,
∴此车超过了太湖大道每小时80千米的限制速度.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
2.一枚质地均匀的骰子,其六个面上分别标有数字1,2,3,4,5,6,投掷一次,朝上一面的数字是偶数的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
4.2015年双11淘宝全天交易额为571亿,将数字57100000000用科学记数法表示为( )
| A. | 5.71×108 | B. | 5.71×1010 | C. | 5.71×109 | D. | 571×108 |
 二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$的图象可能是( )
二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$的图象可能是( )



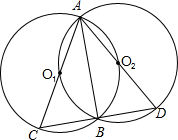 如图,两等圆⊙O1和⊙O2相交于A、B两点,且两圆相互过圆心,过点B作任一直线,分别交⊙O1、⊙O2于C、D两点,接AC、AD.试猜想△ACD的形状,并说明理由.
如图,两等圆⊙O1和⊙O2相交于A、B两点,且两圆相互过圆心,过点B作任一直线,分别交⊙O1、⊙O2于C、D两点,接AC、AD.试猜想△ACD的形状,并说明理由.