题目内容
 如图,点D,E都在△ABC的边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,连结PQ,若DE=6,则PQ的长为
如图,点D,E都在△ABC的边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,连结PQ,若DE=6,则PQ的长为考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:根据等腰三角形三线合一的性质可得AQ=QE,QP=PD,从而判断出PQ是△ADE的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得PQ=
DE.
| 1 |
| 2 |
解答:解:∵∠ABC的平分线垂直于AE,∠ACB的平分线垂直于AD,
∴AQ=QE,QP=PD,
∴PQ是△ADE的中位线,
∴PQ=
DE=
×6=3.
故答案为:3.
∴AQ=QE,QP=PD,
∴PQ是△ADE的中位线,
∴PQ=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.
点评:本题考查了三角形的中位线定理,等腰三角形的判定与性质,熟记等腰三角形的性质然后判断出PQ是△ADE的中位线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的E处,那么AE为
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的E处,那么AE为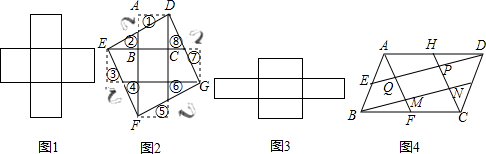
 如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,时间t为( )
如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,时间t为( )