题目内容
9.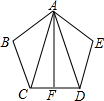 如图,已知AB=AE,BC=ED,∠B=∠E.
如图,已知AB=AE,BC=ED,∠B=∠E.(1)AC=AD吗?为什么?
(2)若点F为CD的中点,那么AF与CD有怎样的位置关系?请说明理由.
分析 (1)根据全等三角形的判定与性质,可得答案;
(2)根据等腰三角形的性质,可得答案.
解答 解:(1)AC=AD,理由如下:
在△ABC和△AED中,
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$,
△ABC≌△AED(SAS),
∴AC=AD;
(2)AF⊥CD,理由如下:
由AC=AD,CF=DF,得
AF⊥CD.
点评 本题考查了全等三角形的判定与性质,熟记圈的那个三角形的判定与性质是解题关键,等腰三角形的性质:等腰三角形的顶角的角平分线,底边的中线,底边的高线三线合一.

练习册系列答案
相关题目
19.若菱形的周长是40,则它的边长为( )
| A. | 20 | B. | 10 | C. | 15 | D. | 25 |
14.已知点M(a,3),点N(2,b)关于x轴对称,则(a+b)2015=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
1.已知用4个矿泉水空瓶可换1瓶矿泉水,现有15个矿泉水空瓶若不再添钱,最多可喝矿泉水( )瓶.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19. 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )
 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )| A. | a-b | B. | a+b | C. | a-2b | D. | 2a-b |




 如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.