题目内容
因式分解：（c2+ab）2-（a+b）2c2= ．
考点：因式分解-运用公式法
专题：
分析：直接利用平方差公式分解因式，进而重新分组进而分解因式．
解答：解：（c2+ab）2-（a+b）2c2
=[（c2+ab）-（a+b）c][（c2+ab）+（a+b）c]
=（c2+ab-ac-bc）（c2+ab+ac+bc）
=[c（c-a）-b（c-a）][c（c+a）+b（c+a）]
=（c-a）（c-b）（a+c）（b+c）．
故答案为：（c-a）（c-b）（a+c）（b+c）．
=[（c2+ab）-（a+b）c][（c2+ab）+（a+b）c]
=（c2+ab-ac-bc）（c2+ab+ac+bc）
=[c（c-a）-b（c-a）][c（c+a）+b（c+a）]
=（c-a）（c-b）（a+c）（b+c）．
故答案为：（c-a）（c-b）（a+c）（b+c）．
点评：此题主要考查了运用公式法以及分组分解法分解因式，正确分组分解因式是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图，AD∥BC，∠1=∠2．求证：∠3+∠4=180°．
如图，在平行四边形ABCD中，EF∥AB，DE：EA=2：5，EF=4，则AB=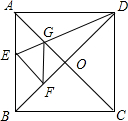
如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后，折叠DE分别交AB、AC于E、G，连接GF，下列结论：下列不等式变形正确的是（ ）
| A、由a＜b，得ac＜bc | ||||
B、由x＞y，且m≠0，得-
| ||||
| C、由x＞y，得xz2＞yz2 | ||||
| D、由xz2＞yz2得x＞y |