题目内容
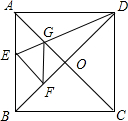 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:①∠FGD=112.5°;②BE=2OG;③S△AGD=S△OGD;④四边形AEFG是菱形.
其中正确结论的序号是
考点:翻折变换(折叠问题),全等三角形的判定,菱形的判定,正方形的性质
专题:证明题
分析:(1)由四边形ABCD是正方形和折叠性得出∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,再由三角形的内角和求出∠FGD=112.5°.故①正确,
(2)由四边形ABCD是正方形和折叠,判断出四边形AEFG是平行四边形,再由AE=EF,得出四边形AEFG是菱形.利用45°的直角三角形得出GF=
OG,BE=
EF=
GF,得出BE=2OG,故②④正确.
(3)由四边形ABCD是正方形和折叠性,得到△ADG≌△FDG,所以S△AGD=S△FDG≠S△OGD故③错误.
(2)由四边形ABCD是正方形和折叠,判断出四边形AEFG是平行四边形,再由AE=EF,得出四边形AEFG是菱形.利用45°的直角三角形得出GF=
| 2 |
| 2 |
| 2 |
(3)由四边形ABCD是正方形和折叠性,得到△ADG≌△FDG,所以S△AGD=S△FDG≠S△OGD故③错误.
解答:解:(1)由四边形ABCD是正方形和折叠性知,
∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,
∴∠FGD=180°-∠DFG-∠FDG=180°-45°-22.5°=112.5°,
故①正确,
(2)由四边形ABCD是正方形和折叠性得出,
∠DAG=∠DFG=45°,∠EAD=∠EFD=90°,AE=EF,
∵∠ABF=45°,
∴∠ABF=∠DFG,
∴AB∥GF,
又∵∠BAC=∠BEF=45°,
∴EF∥AC,
∴四边形AEFG是平行四边形,
∴四边形AEFG是菱形.
∵在RT△GFO中,GF=
OG,
在RT△BFE中,BE=
EF=
GF,
∴BE=2OG,
故②④正确.
(3)由四边形ABCD是正方形和折叠性知,
AD=FD,AG=FG,DG=DG,
在△ADG和△FDG中,
∴△ADG≌△FDG(SSS),
∴S△AGD=S△FDG≠S△OGD
故③错误.
故答案为:①②④.
∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,
∴∠FGD=180°-∠DFG-∠FDG=180°-45°-22.5°=112.5°,
故①正确,
(2)由四边形ABCD是正方形和折叠性得出,
∠DAG=∠DFG=45°,∠EAD=∠EFD=90°,AE=EF,
∵∠ABF=45°,
∴∠ABF=∠DFG,
∴AB∥GF,
又∵∠BAC=∠BEF=45°,
∴EF∥AC,
∴四边形AEFG是平行四边形,
∴四边形AEFG是菱形.
∵在RT△GFO中,GF=
| 2 |
在RT△BFE中,BE=
| 2 |
| 2 |
∴BE=2OG,
故②④正确.
(3)由四边形ABCD是正方形和折叠性知,
AD=FD,AG=FG,DG=DG,
在△ADG和△FDG中,
|
∴△ADG≌△FDG(SSS),
∴S△AGD=S△FDG≠S△OGD
故③错误.
故答案为:①②④.
点评:本题主要考查了折叠问题,菱形的判定及正方形的性质,解题的关键是明确图形折叠前后边及角的大小没有变化.

练习册系列答案
相关题目
锐角三角形的三边长分别是2、3、x,则x的取值范围是( )
A、
| ||||
B、
| ||||
C、1<x<
| ||||
| D、1<x<5 |
 如图9,水平地面上两座建筑物AB、CD,建筑物AB的高度为60米,从建筑物AB的顶端B测得点D的仰角为30°,测得点C的俯角为45°.求建筑物CD的高度.(结果保留根号)
如图9,水平地面上两座建筑物AB、CD,建筑物AB的高度为60米,从建筑物AB的顶端B测得点D的仰角为30°,测得点C的俯角为45°.求建筑物CD的高度.(结果保留根号) 期末考试后,小红将本班50名学生的数学成绩进行分类统计,得到如图所示的扇形统计图,则优生人数为
期末考试后,小红将本班50名学生的数学成绩进行分类统计,得到如图所示的扇形统计图,则优生人数为