题目内容
10. 如图,是一条水平铺设的直径为2米的通水管道横截面,其水面宽度为1.6米,求这条管道中此时水的最大深度.
如图,是一条水平铺设的直径为2米的通水管道横截面,其水面宽度为1.6米,求这条管道中此时水的最大深度.
分析 作出弧AB的中点D,连接OD,交AB于点C.利用垂径定理,以及勾股定理即可求解.
解答  解:作出弧AB的中点D,连接OD,交AB于点C.
解:作出弧AB的中点D,连接OD,交AB于点C.
则OD⊥AB.AC=$\frac{1}{2}$AB=0.8m.
在直角△OAC中,OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{1}^{2}-0.{8}^{2}}$=0.6(m).
则水深CD=OD-OC=1-0.6=0.4(m).
点评 此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.

练习册系列答案
相关题目
20.一次函数y=3x-4的截距是( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
18.如图是正方体表面展开图,如果将其合成原来的正方体如图时,与点重合的两个点应该是( )


| A. | S和Z | B. | T和Y | C. | T和V | D. | U和Y |
5.一元二次方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实根 | B. | 有两个不相等的实根 | ||
| C. | 无实数根 | D. | 有一个根 |
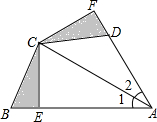 在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,问BE与DF是否相等?为什么?
在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,问BE与DF是否相等?为什么?