题目内容
5．如果两个相似三角形的对应中线的比为2：3，那么这两个相似三角形的周长的比为2：3．分析 根据相似三角形的性质可直接得出结论．
解答 解：∵两个相似三角形的对应中线的比为2：3，
∴其相似比为2：3，
∴这两个相似三角形的周长的比为2：3．
故答案为：2：3．
点评 本题考查的是相似三角形的性质，熟知相似三角形（多边形）的周长的比等于相似比是解答此题的关键．
练习册系列答案
相关题目
15．
张大伯计划建一个面积为72平方米的长方形养鸡场，为了节约材料，鸡场一边靠着原有的一堵墙（墙长15米），另外的部分用26米的竹篱笆围成，如图所示，如果设垂直于墙的一边长为x米，那么x满足的方程是（ ）
张大伯计划建一个面积为72平方米的长方形养鸡场，为了节约材料，鸡场一边靠着原有的一堵墙（墙长15米），另外的部分用26米的竹篱笆围成，如图所示，如果设垂直于墙的一边长为x米，那么x满足的方程是（ ）| A． | x（13-x）=72 | B． | x（26-x）=72 | C． | x$\frac{（26-x）}{2}$=72 | D． | x（26-2x）=72 |
20．一次函数y=3x-4的截距是（ ）
| A． | 4 | B． | -4 | C． | 3 | D． | -3 |
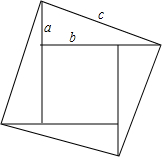如图所示，现用三边长分别为a，b，c的四个全等的直角三角形拼成正方形，利用以下方法验证：a2+b2=c2，在图中，边长为c的大正方形的面积为（a2+b2）或c2．
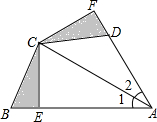在△ABC中，CE⊥AB于E，在△ABC外作∠CAD=∠CAB，过C作CF⊥AD，交AD的延长线于F，且∠FDC=∠B，问BE与DF是否相等？为什么？