题目内容
1.若|x-y|+$\sqrt{y-2}$=0,则xy+1的值为5.分析 依据非负数的性质可求得x、y的值,然后代入计算即可.
解答 解:∵|x-y|+$\sqrt{y-2}$=0,
∴x-y=0,y-2=0,
解得:x=2,y=2.
∴xy+1=4+1=5.
故答案为:5.
点评 本题主要考查的是非负数的性质,熟练掌握非负数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列计算错误的是( )
| A. | $\sqrt{\frac{4}{3}}$÷$\sqrt{\frac{1}{21}}$=2$\sqrt{7}$ | B. | ($\sqrt{8}$+$\sqrt{3}$)×$\sqrt{3}$=2$\sqrt{6}$+3 | C. | (4$\sqrt{2}$-3$\sqrt{6}$)÷2$\sqrt{2}$=2-$\frac{3}{2}$$\sqrt{3}$ | D. | ($\sqrt{5}$+7)($\sqrt{5}$-7)=-2 |
16.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的方差是( )
| A. | $\frac{3}{2}$ | B. | 10 | C. | $\frac{11}{6}$ | D. | $\frac{5}{3}$ |
6.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{15}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{1}{5}}$ | D. | $\sqrt{9}$ |
11.下列说法错误的是( )
| A. | 顺次连接矩形各边的中点所成的四边形是菱形 | |
| B. | 四个角都相等的四边形是矩形 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 一组对边平行且相等的四边形是平行四边形 |
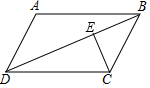 如图,在平行四边形ABCD中,对角线BD=14cm,CE⊥BD,垂足为点E,且CE=5cm,AD=7cm,则AD与BC之间的距离为10cm.
如图,在平行四边形ABCD中,对角线BD=14cm,CE⊥BD,垂足为点E,且CE=5cm,AD=7cm,则AD与BC之间的距离为10cm.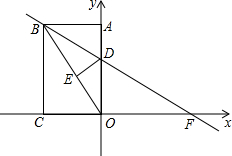 如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(-6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(-6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.