题目内容
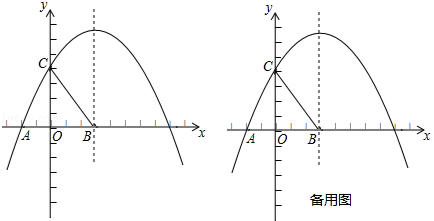
5.如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标.
分析 (1)根据点A的坐标和对称轴得出方程组,解方程组求出a和b即可;
(2)由平行四边形的性质得出BC∥MN,BC=MN.分两种情况:
①N点在M点下方,设M(x,-$\frac{1}{4}$x2+$\frac{3}{2}$x+4),则N(x+3,-$\frac{1}{4}$x2+$\frac{3}{2}$x),由N在x轴上得出-$\frac{1}{4}$x2+$\frac{3}{2}$x=0,解方程即可;
②M点在N点右下方,设M(x,-$\frac{1}{4}$x2+$\frac{3}{2}$x+4),则N(x-3,-$\frac{1}{4}$x2+$\frac{3}{2}$x+8),由N在x轴上得出方程,解方程即可.
解答 解:(1)∵抛物线y=ax2+bx+4交x轴于A(-2,0),
∴0=4a-2b+4,
∵对称轴是直线x=3,
∴-$\frac{b}{2a}$=3,即6a+b=0,
关于a,b的方程联立为$\left\{\begin{array}{l}{4a-2b+4=0}\\{6a+b=0}\end{array}\right.$,
解得 a=-$\frac{1}{4}$,b=$\frac{3}{2}$,
∴抛物线的表达式为y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4;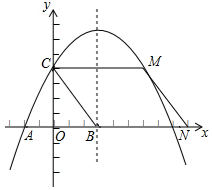
(2)∵四边形为平行四边形,且BC∥MN,
∴BC=MN.
分两种情况:
①N点在M点下方,如图所示:
即M点向下平移4个单位,向右平移3个单位与N重合.
设M(x,-$\frac{1}{4}$x2+$\frac{3}{2}$x+4),则N(x+3,-$\frac{1}{4}$x2+$\frac{3}{2}$x),
∵N在x轴上,
∴-$\frac{1}{4}$x2+$\frac{3}{2}$x=0,
解得 x=0(舍去),或x=6,
∴xM=6,
∴M(6,4);
②M点在N点右下方,即N向下平移4个单位,向右平移3个单位与M重合.
设M(x,-$\frac{1}{4}$x2+$\frac{3}{2}$x+4),则N(x-3,-$\frac{1}{4}$x2+$\frac{3}{2}$x+8),
∵N在x轴上,∴-$\frac{1}{4}$x2+$\frac{3}{2}$x+8=0,
解得 x=3-$\sqrt{41}$,或x=3+$\sqrt{41}$,
∴xM=3-$\sqrt{41}$或3+$\sqrt{41}$.
∴M2(3-$\sqrt{41}$,-4)或M3(3+$\sqrt{41}$,-4).
综上所述,M的坐标为(6,4)或(3-$\sqrt{41}$,-4)或(3+$\sqrt{41}$,-4)
点评 本题是二次函数综合题目,考查了二次函数解析式的求法、平行四边形的性质、平移的性质、解方程等知识;本题综合性强,有一定难度.

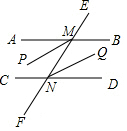 已知:如图,AB∥CD,AB,CD与直线EF分别相交于点M和N,MP平分∠AMF,NQ平分∠DNE.求证:MP∥NQ.
已知:如图,AB∥CD,AB,CD与直线EF分别相交于点M和N,MP平分∠AMF,NQ平分∠DNE.求证:MP∥NQ.