��Ŀ����
7����ƽ��ֱ������ϵxOy�У�������y1=2x2+fx+h������A��0��-2����B��3��4������1����������y1����M�����겢ֱ��д�����߶�AB�·��������ϵĵ㵽�Գ���ľ���d��x������������x��ȡֵ��Χ��
��2�����B����ԭ��ĶԳƵ�ΪC����D��������y1�Գ�����һ���㣬����������A��B֮��IJ���Ϊͼ��G������A��B���㣩����ֱ��CD��ͼ��G�й����㣬��Ϻ���ͼ�����D������t��ȡֵ��Χ��
��3������������y1�����ʵ���ƽ�ƺ��������Ϊy2����������y2�Ķ���պ�����ֱ��AB��ʱ��������y2��ֱ��AB����һ����ǡ���ǵ�B�������ƽ�ƺ�������ߵĶ����Ϊ��N�����ʱ��MNB�������
���� ��1�����ô���ϵ������������߽���ʽ�����䷽�ó��������꣬��ͼ��ֱ�ӵó����������ķ�Χ��
��2����������ͼ��ֱ�ӵó�����������t�ķ�Χ��
��3�������ƽ�ƺ������ߵĽ���ʽ���ɵó�N������꣬���������ʽ��⣮
��� �⣺��1����ͼ1��
��������y1=2x2+fx+h������A��0��-2����B��3��4����
��$\left\{\begin{array}{l}{h=-2}\\{18+3f-2=4}\end{array}\right.$��
��$\left\{\begin{array}{l}{f=-4}\\{h=-2}\end{array}\right.$��
�������߽���ʽΪy1=2x2-4x-2=2��x-1��2-4��
��M��1��-4����
��ͼ��֪���߶�AB�·��������ϵĵ㵽�Գ���ľ���d��x������������x��ȡֵ��ΧΪ1��x��3��
��2����ͼ1��
�ߵ�B��3��4������ԭ��ĶԳƵ�ΪC��
��C��-3��-4����
��CM��x�ᣬ
��ֱ��CD��ͼ��G�й�����ĵ�D��������СֵΪ��M����������-4��
����C��ֱ��BC��
����ͼ��֪��ֱ��BC��ͼ��Gֻ��һ������B��
��ֱ��CD��ͼ��G�й�����ĵ�D���������ֵΪ��B����������4��
���D������t��ȡֵ��ΧΪ��-4��t��4��
��3����ͼ2��
����MN��BM���ɣ�1�������ߵĽ���ʽΪy1=2x2-4x-2=2��x-1��2-4��
��A��0��-2����B��3��4����
��ֱ��AB����ʽΪy=2x-2��
��ֱ��AB��x���ཻ�ڵ�D��1��0�����պ���������y1�ĶԳ�����x��Ľ��㣬
�ߵ�������y2�Ķ���պ�����ֱ��AB��ʱ
����ƽ�ƺ�������ߵĶ����Ϊ��N��n��2n-2����
��ƽ�ƺ�������ߵĽ���ʽΪy2=2��x-n��2+2n-2��
��������y2��ͼ�����B��3��4����
��4=2��3-n��2+2n-2��
��n=2��n=3����N�͵�B�غϲ��ܹ��������Σ���ȥ����
��N��2��2����
��M��1��-4����
��DM=4��
��S��BMN=S��BDM-S��NDM=$\frac{1}{2}$DM��|xB-xD|-$\frac{1}{2}$DM��|xN-xD|=$\frac{1}{2}$��4����3-1��-$\frac{1}{2}$��4����2-1��=2��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ����������ͼ������ʣ������ε�����ļ��㷽�����Ȿ��Ĺؼ��ǻ�������ͼ��

 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�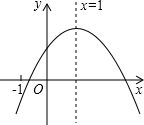 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���Գ�����ֱ��x=1���������ĸ����۴�����ǣ�������
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���Գ�����ֱ��x=1���������ĸ����۴�����ǣ�������| A�� | b��0 | B�� | 2a+b=0 | C�� | b2-4ac��0 | D�� | a-b+c��0 |
| A�� |  | B�� |  | C�� |  | D�� |  |
��ͬλ����ȣ�
��ͬ�ǵ������ȣ�
�����|a|=|b|����ôa=b��
���ڽǵ��ڲ�����ƽ�����ϵĵ㵽�����ߵľ�����ȣ�
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | -4x6 | B�� | -4x7 | C�� | 4x8 | D�� | -4x8 |
| A�� | n | B�� | 2n-2 | C�� | 2n | D�� | 2n+2 |
| A�� | -1��0 | B�� | 3��-2 | C�� | -2��-5 | D�� | 1��-2 |