题目内容
观察图（1）至图（4）及相应推理，其中正确的是（ ）
A、 |
B、 |
C、 |
D、 |
考点：圆周角定理,垂径定理,圆心角、弧、弦的关系
专题：
分析：根据圆心角、弧、弦的关系对A、C进行判断；根据圆周角定理对B进行判断；根据垂径定理对D进行判断．
解答：解：A、∠AOB=∠A′OB′，则AB弧的度数等于A′B′弧的度数，所以A选项错误；
B、由∠AOB=80°得∠ACB=40°，所以B选项错误；
C、由
=
，则
=
，所以AB=CD，所以C选项正确；
D、当OM⊥AE时，弧AM等于ME弧，所以D选项错误．
故选C．
B、由∠AOB=80°得∠ACB=40°，所以B选项错误；
C、由
 |
| AD |
|
| BC |
|
| CD |
|
| AB |
D、当OM⊥AE时，弧AM等于ME弧，所以D选项错误．
故选C．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理和圆心角、弧、弦的关系．
练习册系列答案
高中必刷题系列答案
相关题目
如图，正整数按如图排列，请写出第六行，第六列的数字是线段CD是由线段AB平移得到的，点A（-2，3）的对应点为C（3，6），则点B（-4，-1）的对应点D的坐标为（ ）
| A、（2，9） |
| B、（5，3） |
| C、（1，2） |
| D、（-9，-4） |
数轴上表示-1和
的点分别是A、B，点B关于点A的对称点是C，则点C表示的数是（ ）
| 2 |
A、
| ||
B、1-
| ||
C、-2-
| ||
D、
|
若方程组
与
有相同的解，则a、b的值为（ ）
|
|
| A、2，3 | B、3，2 |
| C、2，-1 | D、-1，2 |
线段A，B两个端点坐标分别为A（-2，4），B（6，-4），则中点坐标为（ ）
| A、（-2，0） |
| B、（0，-2） |
| C、（2，0） |
| D、（0，2） |
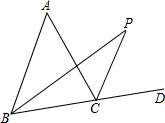如图，D是△ABC的边BC的延长线上一点．∠ABC、∠ACD的平分线相交于P．