题目内容
14.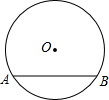 如图是我市环北路改造后一圆柱形输水管的横截面,AB下方部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为2.5m.
如图是我市环北路改造后一圆柱形输水管的横截面,AB下方部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为2.5m.
分析 先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD=$\frac{1}{2}$AB,设OA=r,则OD=r-1,在Rt△AOD中,利用勾股定理即可求出r的值.
解答 解:如图所示:
过点O作OD⊥AB于点D,连接OA,
∵OD⊥AB,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2m,
设OA=r,则OD=r-1,
在Rt△AOD中,OA2=OD2+AD2,即r2=(r-1)2+22,
解得:r=2.5.
故答案为:2.5m.
点评 本题考查的是垂径定理的应用,勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.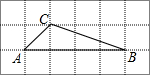 如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
 如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{{\sqrt{10}}}{3}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
3.估计$\sqrt{5}$-1的值在哪两个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
 如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.
如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.