题目内容
5. 如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.
如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.
分析 根据已知条件和特殊角的三角函数值求出BC,再根据tanA=$\frac{2}{5}$,求出AC,最后根据AD=AC-CD,即可得出答案.
解答 解:在△BDC中,
∵∠C=90°,∠BDC=60°,DC=2$\sqrt{3}$,
∴tan60°=$\frac{BC}{DC}$=$\frac{BC}{2\sqrt{3}}$,
∴BC=6,
在△ABC中,
∵tanA=$\frac{2}{5}$,
∴$\frac{BC}{AC}$=$\frac{2}{5}$,
∴AC=15,
∴AD=AC-CD=15-2$\sqrt{3}$.
点评 此题考查了解直角三角形,用到的知识点是特殊角的三角函数值,关键是根据题意求出BC的值.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1>y2.
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
17.某同学在计算“一个整式A减去多项式2a2b-3ab2+5”时,误算成加上这个多项式,得到的结果为ab2+2a2b-3,则整式A为( )
| A. | -4ab2+2 | B. | -2ab2-8 | C. | 4a2b-2ab2+2 | D. | 4ab2-8 |
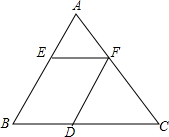 如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长.
如图,△ABC中,EF∥BC,FD∥AB,AE=12,BE=18,AF=14,CD=24,求线段FC,EF的长.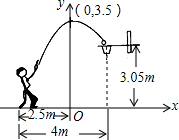 如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.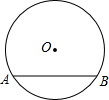 如图是我市环北路改造后一圆柱形输水管的横截面,AB下方部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为2.5m.
如图是我市环北路改造后一圆柱形输水管的横截面,AB下方部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为2.5m. 如图是由5个大小相同的正方体组成的几何体,从正面看到的形状图是( )
如图是由5个大小相同的正方体组成的几何体,从正面看到的形状图是( )


