题目内容
9.将一根长22cm的铁丝,折成一个面积为30cm2的矩形,那么这个矩形的长边是6cm.分析 设这个矩形的长边是xcm,则另一边长是(11-x)cm,根据矩形的面积公式,即可列出一元二次方程求解.
解答 解:设这个矩形的长边是xcm,
根据题意x($\frac{22}{2}$-x)=30,整理得x2-11x+30=0,
解得x1=5,x2=6,
由x1=5得$\frac{22}{2}$-x=6(与题设不符,舍去).
由x2=6得$\frac{22}{2}$-x=5.
则这个矩形的长边是6cm.
故答案为:6.
点评 本题考查了一元二次方程在实际生活中的应用及矩形的面积公式,表示出矩形的长与宽得出方程是解题关键.

练习册系列答案
相关题目
19.在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )
| A. | 14.4 | B. | 19.2 | C. | 18.75 | D. | 17 |
17.如果一个角的补角等于它余角的4倍,那么这个角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
18.“南海”在过去的2016年中出镜率非常高,为了让学生了解南海,关注南海.某校举办了南海有关知识比赛,唐老师对名列前20名的选手的得分x进行分组统计,结果如表所示:
(1)求b的值
(2)若用扇形图来描述,求分值在8≤m<9范围内所对应的扇形图的圆心角大小;
(3)若唐老师从第一粗和第三组这4名同学中随机选取2名同学进行座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果)
| 组号 | 分值 | 频数 |
| 一 | 6≤m<7 | 2 |
| 二 | 7≤m<8 | 8 |
| 三 | 8≤m<9 | a |
| 四 | 9≤m≤10 | b |
(2)若用扇形图来描述,求分值在8≤m<9范围内所对应的扇形图的圆心角大小;
(3)若唐老师从第一粗和第三组这4名同学中随机选取2名同学进行座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果)
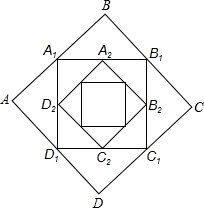 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是$\sqrt{2}$.
如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是$\sqrt{2}$.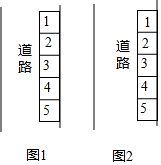 小明和小丽所在生活小区的管理人员为了方便业主合理规范摆放机动车,在小区内部道路的一侧按照标准画出了一些停车位.
小明和小丽所在生活小区的管理人员为了方便业主合理规范摆放机动车,在小区内部道路的一侧按照标准画出了一些停车位.