题目内容
19.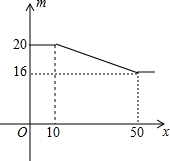 我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元
我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元(1)写出当10<x≤50时,售出的单价m(元/个)与顾客一次购买的数量x(个)之间的函数关系式;
(2)写出该专卖店一次销售这种计算器x个时,所获利润y(元)与x(个)之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的个数在10至50个之间,问一次卖多少个获得的利润最大?其最大利润为多少?
分析 (1)把点(10,20),(50,16)分别代入一次函数y=kx+b(k≠0),列出关于系数k、b的方程组,通过解方程组可以求得它们的值;
(2)根据购买的数量的不同有不同的优惠方法,故本题时一个分段函数,注意自变量的取值范围;
(3)列出有关购买只数的二次函数求其最大值即可,可以采用配方法求其最值,也可以用公式求其最值.
解答 解:(1)设y=kx+b(k≠0),把点(10,20),(50,16)分别代入,得
$\left\{\begin{array}{l}{10k+b=20}\\{50k+b=16}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=21}\end{array}\right.$,
所以该函数解析式是:y=-$\frac{1}{10}$x+21(10<x≤50);
(2)当0<x≤10时,y=20x-13x=7x,即y=7x.
当10<x≤50时,(20-13)x-0.1(x-10)x=-$\frac{1}{10}$x2+8x.即y=-$\frac{1}{10}$x2+8x.
当x>50时,y=16x-13x=3x,即y=3x.
综上所述,y=$\left\{\begin{array}{l}{7x(0<x≤10)}\\{-\frac{1}{10}{x}^{2}+8x(10<x≤50)}\\{3x(x>50)}\end{array}\right.$.
(3)将y=-$\frac{1}{10}$x2+8x配方,得
y=-$\frac{1}{10}$(x-40)2+160,
∴店主一次卖40只时可获得最高利润,最高利润为160元.(也可用公式法求得)
点评 本题考查了一次函数的应用,特别是题目中的分段函数,一定要注意自变量的取值范围.

 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=35°,则∠A=( )
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=35°,则∠A=( )| A. | 70° | B. | 80° | C. | 55° | D. | 65° |
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF=( )| A. | 4:9 | B. | 1:4 | C. | 1:2 | D. | 1:1 |
| A. | 4cm | B. | 5cm | C. | 6cm | D. | 13cm |
| A. | y=0.12x,x>0 | B. | y=60-0.12x,x>0 | ||
| C. | y=0.12x,0≤x≤500 | D. | y=60-0.12x,0≤x≤500 |
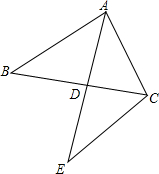 已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.
已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.
