题目内容
1.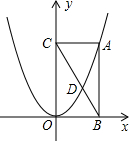 如图,点A在二次函数y=ax2(a>O)第一象限的图象上,AB⊥x轴,AC⊥y轴,垂足分别为B,C,连接BC.交函数图象于点D,则$\frac{CD}{CB}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,点A在二次函数y=ax2(a>O)第一象限的图象上,AB⊥x轴,AC⊥y轴,垂足分别为B,C,连接BC.交函数图象于点D,则$\frac{CD}{CB}$的值为$\frac{\sqrt{5}-1}{2}$.
分析 设A(m,am2),则B(m,0),C(0,am2),根据待定系数法求得直线BC的解析式,然后联立方程求得D的坐标即可求得$\frac{CD}{CB}$的值.
解答 解:设A(m,am2),则B(m,0),C(0,am2),
设直线y=kx+b,
∴$\left\{\begin{array}{l}{mk+b=0}\\{b=a{m}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-am}\\{b=a{m}^{2}}\end{array}\right.$,
∴y=-amx+am2,
解$\left\{\begin{array}{l}{y=-amx+a{m}^{2}}\\{y=a{x}^{2}}\end{array}\right.$得x1=$\frac{\sqrt{5}-1}{2}m$,x2=$\frac{-\sqrt{5}-1}{2}$m(舍去),
∴$\frac{CD}{CB}$=$\frac{\frac{\sqrt{5}-1}{2}m}{m}$=$\frac{\sqrt{5}-1}{2}$.
故答案为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了二次函数图象上点的坐标特征,待定系数法求一次函数的解析式以及二次函数和一次函数的交点问题,求得D的坐标是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
11.一元一次不等式x+1<2的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
12.关于x的一元二次方程2x2-4xsinα+1=0有两个相等的实数根,则锐角α的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.在5张卡片上分别写有$\frac{7}{13}$,π,$\sqrt{12}$,-0.$\stackrel{•}{6}\stackrel{•}{5}$,0五个数,从中任意抽取一张卡片上的数为无理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |