题目内容
10.在5张卡片上分别写有$\frac{7}{13}$,π,$\sqrt{12}$,-0.$\stackrel{•}{6}\stackrel{•}{5}$,0五个数,从中任意抽取一张卡片上的数为无理数的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由在5张卡片上分别写有$\frac{7}{13}$,π,$\sqrt{12}$,-0.$\stackrel{•}{6}\stackrel{•}{5}$,0五个数,无理数的是π,$\sqrt{12}$,直接利用概率公式求解即可求得答案.
解答 解:∵在5张卡片上分别写有$\frac{7}{13}$,π,$\sqrt{12}$,-0.$\stackrel{•}{6}\stackrel{•}{5}$,0五个数,无理数的是π,$\sqrt{12}$,
∴从中任意抽取一张卡片上的数为无理数的概率是:$\frac{2}{5}$.
故选B.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了1000次,其中有200次摸到白球,因此小亮估计口袋中的红球大约为( )
| A. | 60个 | B. | 50个 | C. | 40个 | D. | 30个 |
18.在下列图象中,能作为一次函数y=-x+1的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{9}$ | D. | $\sqrt{7}$ |
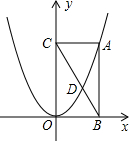 如图,点A在二次函数y=ax2(a>O)第一象限的图象上,AB⊥x轴,AC⊥y轴,垂足分别为B,C,连接BC.交函数图象于点D,则$\frac{CD}{CB}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,点A在二次函数y=ax2(a>O)第一象限的图象上,AB⊥x轴,AC⊥y轴,垂足分别为B,C,连接BC.交函数图象于点D,则$\frac{CD}{CB}$的值为$\frac{\sqrt{5}-1}{2}$.