题目内容
9.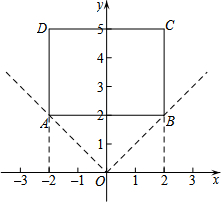 在平面直角坐标系xOy中,对图形W给出如下定义:若图形W上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形ABCD的坐标角度是90°.
在平面直角坐标系xOy中,对图形W给出如下定义:若图形W上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形ABCD的坐标角度是90°.(1)已知点A(0,-3),B(-1,-1),在点C(2,0),D(-1,0),E(2,-2)中,选一点,使得以该点及点A,B为顶点的三角形的坐标角度为90°,则满足条件的点为D(-1,0)和E(2,-2);
(2)将函数y=ax2(1≤a≤3)的图象在直线y=1下方的部分沿直线y=1向上翻折,求所得图形坐标角度m的取值范围;
(3)记某个圆的半径为r,圆心到原点的距离为l,且l=3(r-1),若该圆的坐标角度60°≤m≤90°.直接写出满足条件的r的取值范围.
分析 (1)根据图形的坐标角度的定义画出图形即可解决问题.
(2)分a=1和a=3两种情形画出图形,根据图形的坐标角度的定义即可解决问题.
(3)分m=60°和m=90°两种情形分别讨论即可解决.
解答 解:(1)如图1中,由图象可知,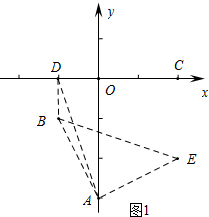
∵∠DOA=90°,∠BOE=90°
∴满足条件的点为D(-1,0),E(2,-2).
故答案为D(-1,0),E(2,-2).
(2)当a=1时,如图2中,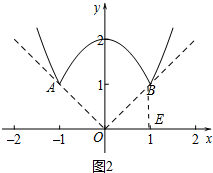
∵角的两边分别过点A(-1,1),B(1,1),作BE⊥x轴于E,
∴BE=OE,
∴∠BOE=45°,
根据对称性可知∠AOB=90°
∴此时坐标角度m=90°;
当a=3时,如图3中,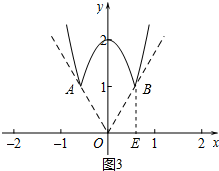
角的两边分别过点A(-$\frac{\sqrt{3}}{3}$,1),B($\frac{\sqrt{3}}{3}$,1),作BE⊥x轴于E,
∵tan∠BOE=$\frac{\sqrt{3}}{3}$,
∴∠BOE=60°,
根据对称性可知∠AOB=60
∴此时坐标角度m=60°,
∴60°≤m≤90°;
(3)∵该圆的坐标角度60°≤m≤90°,圆心到原点的距离为l,
当m=60°时,l=2r,
∵l=3(r-1),
∴2r=3(r-1),
∴r=3,
当m=90°时,l=$\sqrt{2}$r,
∵l=3(r-1),
∴$\sqrt{2}$r=3(r-1),
∴r=$\frac{9+3\sqrt{2}}{7}$,
∴$\frac{9+3\sqrt{2}}{7}$≤r≤3.
点评 本题考查二次函数综合题、图形的坐标角度的定义、圆等知识,解题的关键是理解题意,学会正确画出图形,学会利用特殊点或特殊位置解决问题,属于中考常压轴题.

练习册系列答案
相关题目
19.下列等式成立的是( )
| A. | -22=2-2 | B. | -22=($\frac{1}{2}$)-2 | C. | (-2)-2=22 | D. | (-2)-2=($\frac{1}{2}$)2 |
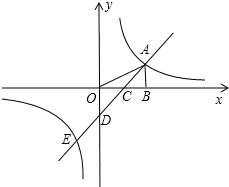 如图,在平面直角坐标系中,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
如图,在平面直角坐标系中,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.