题目内容
13.解方程组$\left\{\begin{array}{l}{3x-4y+5z=3}\\{2x-2y+3z=4}\\{4x+y-2z=2}\end{array}\right.$.分析 先把③×2+②和③×4+①消去y,再解二元一次方程组即可.
解答 解:$\left\{\begin{array}{l}{3x-4y+5z=3①}\\{2x-2y+3z=4②}\\{4x+y-2z=2③}\end{array}\right.$,
③×2+②得:10x-z=8④,
③×4+①得:19x-3z=11⑤,
④×3-⑤得:x=$\frac{13}{11}$,
把x=$\frac{13}{11}$代入④得:z=$\frac{42}{11}$,
把$x=\frac{13}{11},z=\frac{42}{11}$代入③得:y=$\frac{54}{11}$,
所以方程组的解是:$\left\{\begin{array}{l}{x=\frac{13}{11}}\\{y=\frac{54}{11}}\\{z=\frac{42}{11}}\end{array}\right.$
点评 本题考查了解三元一次方程组,解题的关键是掌握消元思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列运算正确的是( )
| A. | (x+y2)2=x2+y4 | B. | b6÷b2=b3 | C. | -a2+2a2=a2 | D. | (2y)2×(-y)=-2y3 |
2. 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )| A. | 44° | B. | 45° | C. | 46° | D. | 54° |
 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
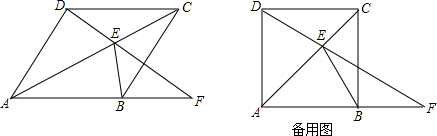
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )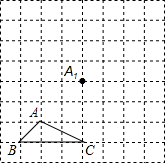 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上). 在平面直角坐标系xOy中,抛物线y=ax2+bx+1经过A(1,3),B(2,1)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+1经过A(1,3),B(2,1)两点.