Question

5．在平面直角坐标系xOy中，抛物线y=ax²+bx+1经过A（1，3），B（2，1）两点．
（1）求抛物线及直线AB的解析式；
（2）点C在抛物线上，且点C的横坐标为3．将抛物线在 点A，C之间的部分（包含点A，C）记为图象G，如果图象G沿y轴向上平移t（t＞0）个单位后与直线  AB只有一个公共点，求t的取值范围．

Answer 1

分析 （1）把点A、B分别代入二次函数解析式，列出关于a、b的方程组，通过解方程组求得系数a、b的值；同理，求得直线方程；
（2）结合图象解题．

解答 解：（1）∵抛物线y=ax²+bx+1经过A（1，3），B（2，1）两点．
∴$\left\{\begin{array}{l}{a+b+1=0}\\{4a+2b+1=1}\end{array}\right.$，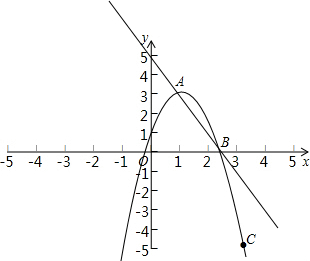
解得，$\left\{\begin{array}{l}{a=-2}\\{b=4}\end{array}\right.$．
∴抛物线的表达式是y=-2x²+4x+1．
设直线AB的表达式是y=mx+n，
∴$\left\{\begin{array}{l}{m+n=3}\\{2m+n=1}\end{array}\right.$，
解得，$\left\{\begin{array}{l}{m=-2}\\{n=5}\end{array}\right.$，
∴直线AB的表达式是y=-2x+5；

（2）∵点C在抛物线上，且点C的横坐标为3．
∴C（3，-5）．
点C平移后的对应点为点C′（3，t-5），代入直线表达式y=-2x+5，
解得t=4．
结合图象可知，符合题意的t的取值范围是0＜t≤4．

点评 本题考查了待定系数法求函数解析式，二次函数图象的几何变换，要熟练掌握画图的能力和识别图形的能力．