题目内容
9.观察:$\frac{1}{1×2}$=1-$\frac{1}{2}$
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$
…
那么$\frac{1}{n×(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$
利用上面的规律计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$=$\frac{99}{100}$.
分析 根据已知等式得出拆项方法,写出规律;原式利用得出的规律变形,计算即可得到结果.
解答 解:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{99}$-$\frac{1}{100}$=1-$\frac{1}{100}$=$\frac{99}{100}$.
故答案为:$\frac{1}{n}$-$\frac{1}{n+1}$;$\frac{99}{100}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.若关于x的一元二次方程x2+2x-k+$\frac{1}{2}$=0总有实数根,则k的取值范围是( )
| A. | k>-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k≤-$\frac{1}{2}$ | D. | k≥-$\frac{1}{2}$ |
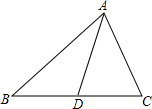 如图,AD是△ABC的中线,若AB=8cm,AC=6cm,则△ABD和△ACD的周长之差为2cm.
如图,AD是△ABC的中线,若AB=8cm,AC=6cm,则△ABD和△ACD的周长之差为2cm.