题目内容
7.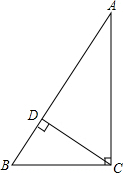 已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
分析 在直角三角形ABC中,利用勾股定理求出AB的长,再利用面积法求出CD的长即可.
解答 解:在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,
由勾股定理得:AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=10,
∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{8×6}{10}$=4.8.
点评 此题考查了勾股定理,以及三角形面积求法,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
18. 下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
(1)李刚6次成绩的极差是10分;中位数是90分.
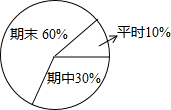
(2)如果用如图的权重给李刚打分,他应该得多少分?
 下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
下表是李刚一学期数学成绩记录,根据信息回答下面的问题:| 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
| 成绩 | 88 | 86 | 90 | 92 | 90 | 96 |
(2)如果用如图的权重给李刚打分,他应该得多少分?
16.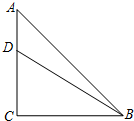 如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )
如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )
 如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )
如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
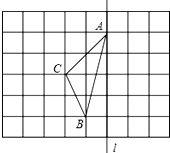 如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.