题目内容
1.已知直线L过点(2,4),且与两坐标轴围成等腰三角形.求:(1)该直线的函数解析式;
(2)所得三角形的周长和面积.
分析 (1)根据题意得出直线L的斜率为±1,设直线L的析式为y=-x+b,代入(2,4)点,根据待定系数法即可求得解析式;
(2)根据解析式求得与坐标轴的交点坐标,然后根据勾股定理求得斜边的长,即可求得周长和面积.
解答 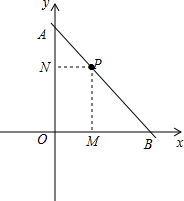 解:(1)∵直线L与两坐标轴围成等腰三角形,
解:(1)∵直线L与两坐标轴围成等腰三角形,
∴直线L的斜率为±1,
设直线L的解析式为y=±x+b,
∵直线L过(2,4)点,
∴4=±2+b,
解得b=6或b=2,
∴该直线的函数解析式为y=-x+6或y=x+2;
(2)①∵直线L的函数解析式为y=-x+6,
∴令y=0,则x=6,令x=0,则y=6,
∴直线L与坐标轴的交点为(6,0)和(0,6),
∴OA=OB=6,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=6$\sqrt{2}$,
∴所得三角形的周长=6+6+6$\sqrt{2}$=12+6$\sqrt{2}$,
面积=$\frac{1}{2}$×6×6=18;
②∵直线L的函数解析式为y=x+2,
∴令y=0,则x=2,令x=0,则y=-2,
∴直线L与坐标轴的交点为(-2,0)和(0,2),
∴OA=OB=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$,
∴所得三角形的周长=2+2+2$\sqrt{2}$=4+2$\sqrt{2}$,
面积=$\frac{1}{2}$×2×2=2.
故所得三角形的周长为12+6$\sqrt{2}$或4+2$\sqrt{2}$,面积是18或2.
点评 本题考查了待定系数法求一次函数的解析式,根据题意求得直线的斜率是解题的关键.

练习册系列答案
相关题目
16.用代入法解方程组$\left\{\begin{array}{l}{x-2y=5①}\\{5x+y=3②}\end{array}\right.$,以下各式正确的是( )
| A. | x-2(3-5x)=2 | B. | x-5=2(3-5x) | C. | 5x+(x-5)=3 | D. | 5x(x-5)=6 |
 如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.
如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD. 一个正方体的表面涂满了同种颜色,按如图所示将它切成27个大小相等的小立方块.设其中仅有i个面(1,2,3)涂有颜色的小立方块的个数为xi,则x1、x2、x3之间的数量关系为x1-x2+x3=2.
一个正方体的表面涂满了同种颜色,按如图所示将它切成27个大小相等的小立方块.设其中仅有i个面(1,2,3)涂有颜色的小立方块的个数为xi,则x1、x2、x3之间的数量关系为x1-x2+x3=2.