题目内容
1.有长为32米的篱笆,一面利用墙(墙的最大可用长度为16米) 围成一个长方形花圃,并在与墙平行的一边开一个1米宽的门.(1)设长方形靠墙的宽为x米,试用x表示长方形的长,并求出x的取值范围;
(2)现在建一个面积为130m2的花圃,求x的值;
(3)当x为多少时,花圃的面积最大?
分析 (1)长方形靠墙的宽为x米,则长方形的长为(32+1-2x)米;
(2)根据长方形面积公式列方程即可解决;
(3)列出花圃的面积与x的函数关系式,利用二次函数的性质即可解答.
解答 解:(1)设长方形靠墙的宽为x米,则长方形的长为(32+1-2x)=33-2x米,
因为0<33-2x≤16,
所以8.5≤x<16.5;
(2)根据题意列方程得:
x(33-2x)=130
解得:x1=6.5(不合题意,舍去),x2=10,
所以当x=10m时,花圃的面积为130m2;
(3)设花圃的面积为S,则
S=x(33-2x)=-2x2+33x=-2(x-8.25)2+136.125,
所以当x=8.25米时,花圃的面积最大.
点评 本题考查了二次函数和一元二次方程的实际应用,根据题目的条件,合理地建立函数关系式是解题关键.

练习册系列答案
相关题目
3.下列式子计算结果为x2-4的是( )
| A. | (x+1)(x-4) | B. | (x+2)(x-2) | C. | (x+2)(2-x) | D. | (x-2)2 |
4.下列计算正确的是( )
| A. | a2+a2=a4 | B. | (-a)2-a2=0 | C. | a8÷a2=a4 | D. | a2•a3=a6 |
1.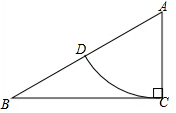 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )
 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )| A. | 1+π | B. | 2+$\frac{π}{2}$ | C. | 1$+\frac{2π}{3}$ | D. | 2+$\frac{π}{3}$ |
13. 如图,BE,CF分别是△ABC的高,M为BC的中点,EF=5,BC=10,则△EFM的周长是( )
如图,BE,CF分别是△ABC的高,M为BC的中点,EF=5,BC=10,则△EFM的周长是( )
 如图,BE,CF分别是△ABC的高,M为BC的中点,EF=5,BC=10,则△EFM的周长是( )
如图,BE,CF分别是△ABC的高,M为BC的中点,EF=5,BC=10,则△EFM的周长是( )| A. | 21 | B. | 18 | C. | 13 | D. | 15 |
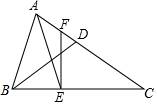 如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为6.
如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为6.