题目内容
20.由下列条件不能判定△ABC为直角三角形的是( )| A. | ∠A+∠C=∠B | B. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | C. | (b+a)(b-a)=c2 | D. | ∠A:∠B:∠C=5:3:2 |
分析 由三角形内角和定理得出条件A和B是直角三角形,由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可得出条件C是直角三角形,B不是;即可得出结果.
解答 A、∵∠A+∠C=∠B,
∴∠B=90°,
故是直角三角形,正确;
B、设a=20k,则b=15k,c=12k,
∵(12k)2+(15k)2≠(20k)2,
故不能判定是直角三角形;
C、∵(b+a)(b-a)=c2,
∴b2-a2=c2,
即a2+c2=b2,
故是直角三角形,正确;
D、∵∠A:∠B:∠C=5:3:2,
∴∠A=$\frac{5}{10}$×180°=90°,
故是直角三角形,正确.
故选:B.
点评 本题考查勾股定理的逆定理、三角形内角和定理;熟练掌握三角形内角和定理和勾股定理的逆定理是证明直角三角形的关键,注意计算方法.

练习册系列答案
相关题目
11.下列各数中,是负分数的是( )
| A. | $\frac{1}{3}$ | B. | -8 | C. | 3.2 | D. | -0.1 |
12.下列函数中,当x<0时,y随x的增大而减小的是( )
| A. | y=$\frac{3}{4}$x | B. | y=x-1 | C. | y=x2 | D. | y=-x2 |
9.下列结论正确的是( )
| A. | 有理数包括正数和负数 | B. | 0是最小的整数 | ||
| C. | 无限不循环小数叫做无理数 | D. | 数轴上原点两侧的数互为相反数 |
10.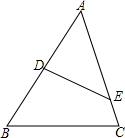 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠AED=∠C |
 如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F
如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F